网站维护
系统内容更新/升级中

Would you like to predict organic reaction outcomes accurately? Design synthetic sequences with higher rate of success?
Would you prefer to learn and rationalize organic chemistry in a data-driven manner?
Please join us to unleash the magical power of Quantum Mechanics (QM).
We learned that nucleophilic substitution of 2,4-dichloro-5-methylpyrimidine with a nucleophile, such as piperidine, proceeds preferentially at C-4 position (Figure 1). Intuitively it makes more sense for the substitution to occur faster at C-2, which has two electron withdrawing aromatic nitrogen atoms next to it. Why is it not the case? We also observed that when the nucleophile is alkyllithium, a C-6 addition product is observed instead of C-4 displacement of chloride. Why?

The question becomes “What could be the best scientific method to rationalize, to learn these chemistry?” In our synthetic organic chemistry laboratories, we found QM to be the most valid and efficient tool for these purposes. In this article, we will discuss how we use LUMO and LUMO Map to analyze nucleophilic aromatic substitution reactions. You will see that it is relatively easy to understand and apply QM in your laboratories.
First let's review the basics of Molecular Orbital (MO) Theory, which proposes that when atoms come together to constitute a molecule, their atomic orbitals interact with each other and form new molecular orbitals. These orbitals have their own energy levels and unique spatial distribution. For organic reaction, we could focus on the use of Frontier Molecular Orbital (FMO) Theory, which emphasizes the analyses with outer orbitals, i.e., Highest Occupied Molecular Orbital (HOMO) and the Lowest Unoccupied Molecular Orbital (LUMO). Based on FMO theory, an organic reaction is electron transfer from nucleophilic part (HOMO) to the electrophilic part (LUMO) of the reacting system. It enables chemists to understand how orbitals interact with one another throughout the course reactions, and to account for chemical reactivity & selectivity observed, etc.
Now let’s use FMO theory to rationalize the aforementioned nucleophilic reactions with the dichloropyrimidine (Figure 1).
There are a number of powerful QM computing tools available to us. Our laboratory chemists prefer to use Spartan, which has a user-friendly graphic interface, making calculations relatively easy to set up and the results easier to interpret.
First, let’s calculate the LUMO and its associated orbital energies of 2,4-dichloro-5methylpyrimidine (the electrophile in the reaction) with Spartan (Figure 2).
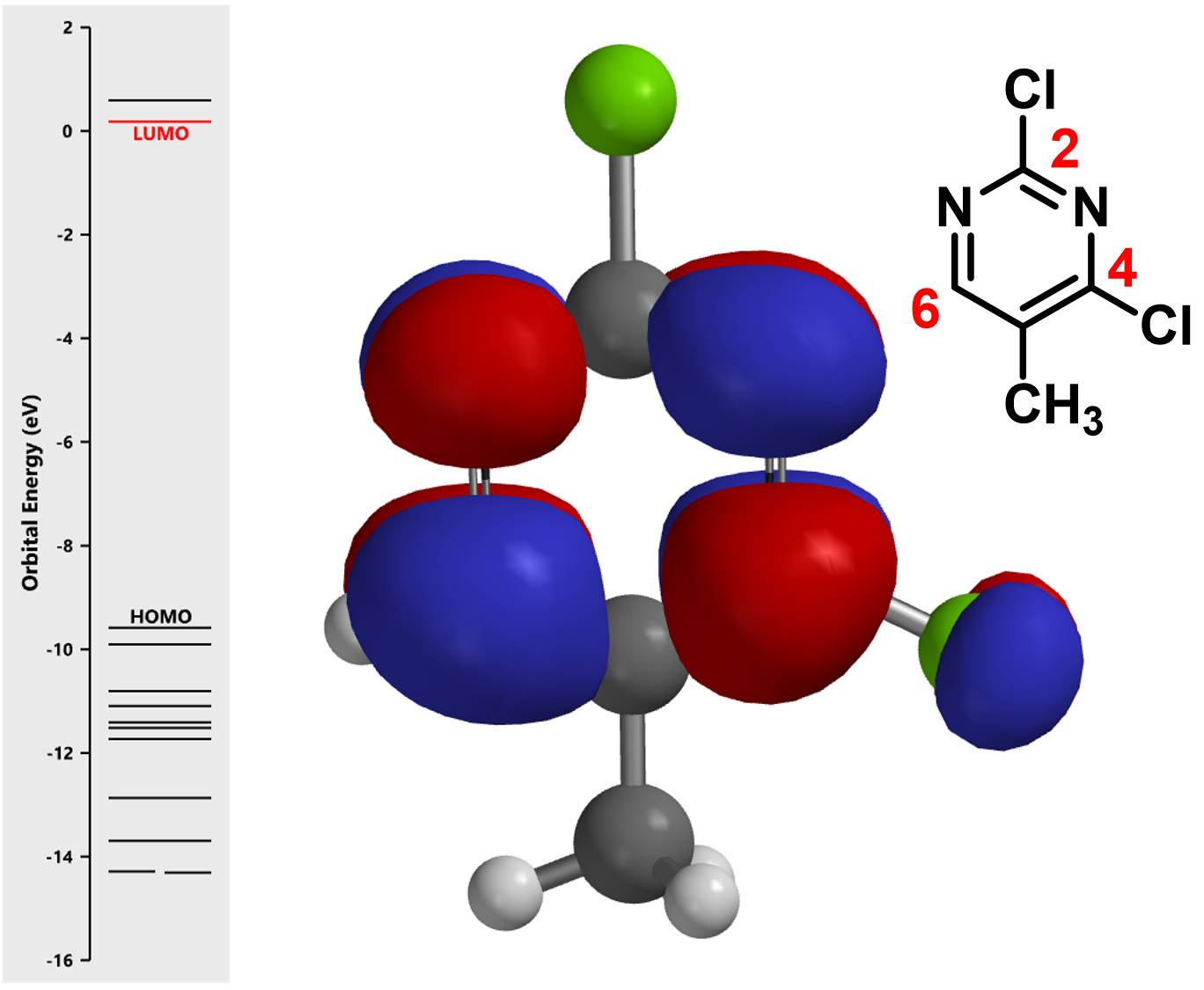
Notice that there is no LUMO lobe over C-2, as such, accounting for no displacement reaction observed at this carbon. Whereas at C-4 and C-6, both have LUMO lobes associated with them, as such these LUMO lobes will be able to interact with incoming nucleophiles. Moreover, addition of piperidine at C-6 site is reversible, while addition at C-4 site will lead to displacement of the chloro group, an irreversible event. That leads to the overall transformation we observed (Figure 3).
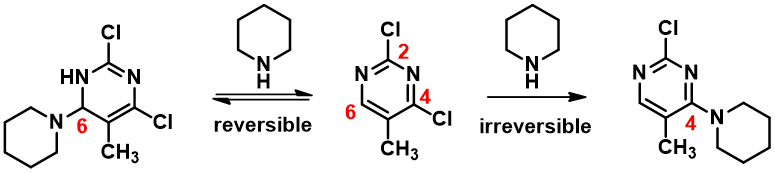
Then why treatment of 2,4-dichloro-5-methylpyrimidine with n-butyllithium affords only the C-6 addition product? It is the same substrate, same LUMO.
To understand this, we calculated for the LUMO Map, which is a superposition of LUMO and Electron Density Map of the molecule. This provides us a quantitative comparison of which part of the molecule is more accessible to attack by an incoming nucleophiles. In the default settings of Spartan, colors near red indicates that the LUMO energy at this location is close to zero, i.e., a low probability of being attacked. On the contrary, colors near blue indicates a much higher energy level, suggesting that the LUMO lobe at this location is highly accessible.
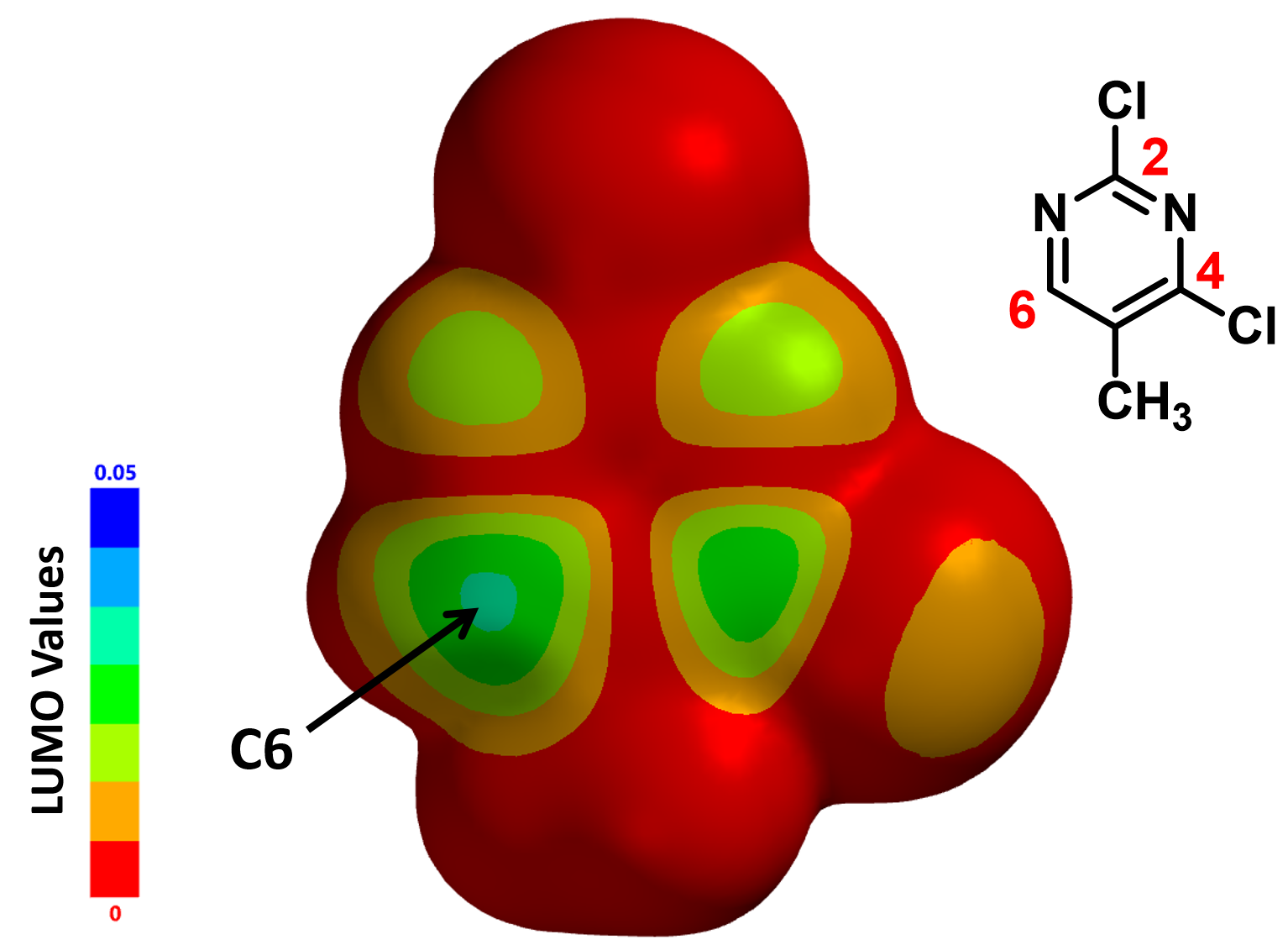
With the LUMO Map of 2,4-dichloro-5-methylpyrimidine (Figure 4), it becomes obvious that the C-6 position is more accessible to nucleophilic attack than the C-4 carbon. Furthermore, addition of n-butyllithium at C-6 site is irreversible, as such, we could only observe the C-6 addition product. This is a highly selective addition reaction under kinetic control (Figure 5).

In summary, we integrate QM (calculated LUMO, LUMO Map), our knowledge of the inherent properties of different nucleophiles, and the stability of their addition products, to rationalize this set of pyrimidine chemistry. And we learned that knowledge gained from retrospective analyses of our chemistry with QM enables us to transform it into a powerful prospective tool.
If the methyl group in the substrate (2,4-dichloro-5-methylpyrimidine) is replaced with Cl, Br, CF3, and CCl3, which position do you think an aliphatic amine will attack, respectively? What is your rationale behind? (Hint: Compare their LUMOs. The CCl3 analog is unique. )
With our next article, we will discuss the application of HOMO to rationalize (then predict) the regio-selectivity of heterocyclic electrophilic reactions.
This article is written and edited by Qiuyue Wang, Guqin Shi, John S. Wai.
References:
[1] Warren J. Hehre (2003). A Guide to Molecular Mechanics and Quantum Chemical Calculations. Irvine, CA, USA: Wavefunction, Inc.
[2] J. A. Joule & K. Mills (2000). Heterocyclic Chemistry. The Diazines: Pyridazine, Pyrimidine, and Pyrazine: Reactions and Syntheis.