在第七章《LUMO运用进阶》的“小试牛刀”部分，我们介绍了 McDonald等人在2006年报道的一类独特的远程取代反应 (tele-substitution)^[1]：2,3-二氯吡嗪与锂化二硫缩醛发生取代反应，生成吡嗪C6位氢原子被亲核试剂取代，同时其对位C3上的氯原子被氢原子取代的产物。这一反应结果与我们熟悉的2,3-二氯吡嗪与其它亲核试剂（如胺、烯醇负离子等）的反应结果相矛盾^[2]。例如，2,3-二氯吡嗪与锂化的苯丁酮反应会得到C2位氯被取代的产物（图1）。

图1. 2,3-二氯吡嗪参与的C2、C6位亲核取代反应

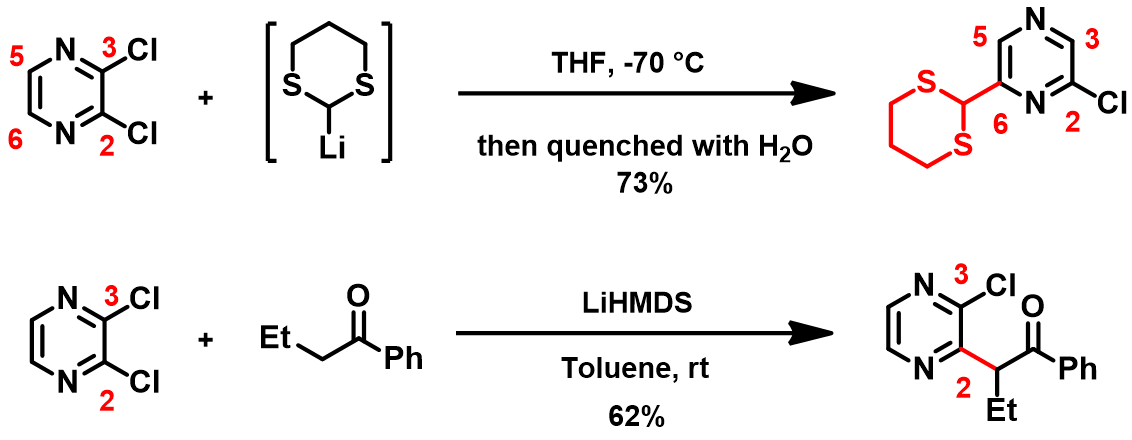
怎么来解释2,3-二氯吡嗪在这两个反应中不同的位点选择性呢？2,3-二氯吡嗪与锂化二硫缩醛的反应中，C3的氯又是如何离去的呢？

接下来，就让我们一起利用第一章和第七章学到的LUMO和LUMO Map来试着分析这个反应过程吧。

利用LUMO & LUMO Map预测亲核反应位点

首先，计算2,3-二氯吡嗪的LUMO和LUMO map示意图（图2）。

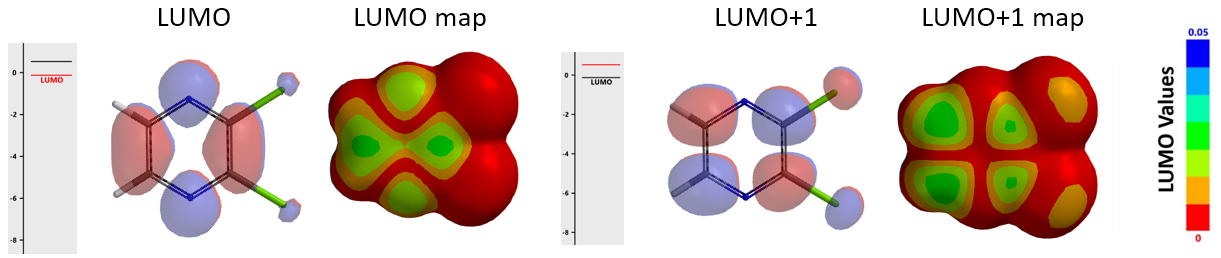
图2. 2,3-二氯吡嗪的LUMO/LUMO map（左）及LUMO+1/LUMO+1 map（右）

如图2所示，2,3-二氯吡嗪的LUMO lobes主要位于C2和C3，C5和C6（红色）之间，而不是四个碳原子上。同时，其LUMO与LUMO+1能级的能量差只有0.65 eV，所以有必要进一步分析LUMO+1能级。可以看到在该能级下C2/C3和C5/C6都有明显的lobe覆盖，且大小大致相等。 LUMO+1 map显示，C5/C6的LUMO+1 lobes比C2/C3更加暴露于分子表面（由于Cl取代基的影响），所以C5/C6被亲核进攻的概率更大。

反应可逆性对于反应结果的影响

根据LUMO+1/LUMO+1 map结果，我们可以预测当2,3-二氯吡嗪与烯醇锂盐反应时（图3），亲核试剂优先进攻C6，其次才是C2；但是，由于C6位的加成反应是可逆的，而C2位的反应是不可逆的。所以，反应最终得到的是C2位氯被取代的产物。

图3. 2,3-二氯吡嗪与烯醇锂盐的亲核取代反应

当亲核试剂换成锂化二硫缩醛（图4），同样，亲核试剂优先进攻C6，而这一反应是不可逆的，所以得到C6位取代的主产物。

图4. 2,3-二氯吡嗪与锂化二硫缩醛的亲核取代反应

通过以上的分析，我们知道了进攻的可逆或不可逆导致了2,3-二氯吡嗪与亲核试剂反应得到不同位点的取代产物。细心的小伙伴可能发现了在与锂化二硫缩醛的反应中，2,3-二氯吡嗪6位被取代的同时，C3位的氯原子悄悄的离开了。这是怎么回事呢？

Cl消除机理

我们提出了如图5所示的反应机理。首先，2,3-二氯吡嗪与锂化二硫缩醛不可逆的生成负离子中间体I以及共振结构I’和I’’；用水淬灭后，负离子中间体获得一个质子形成化合物B，B有四种可能的结构；化合物B消除一分子HCl得到芳构化的产物C。

图5. 2,3-二氯吡嗪与锂化二硫缩醛的亲核取代反应机理

中间体B的消除历程到底从哪个结构发生呢？如图6所示，使用DFT计算得到四种异构体B1，B2，B3和B4的分布比例大约为0 : 0.8 : 7.2 : 91.9。其中，B1能量最高，其分布几乎为零。异构体B4由于存在N=C-C=N的共轭体系，它的相对能量最低为 -6.53 kcal/mol，分布比例也最高，但是两个氯原子都连接在sp²杂化的碳原子上，不能发生HCl消除的反应。B2和B3中没有这种共轭体系，但是B2和B3中氯原子连接在sp³杂化碳上，可以发生消除反应。那么哪个结构优先发生接下来的消除反应呢？这里我们需要请出老朋友——反应能量变化曲线（Reaction Energy Profile）。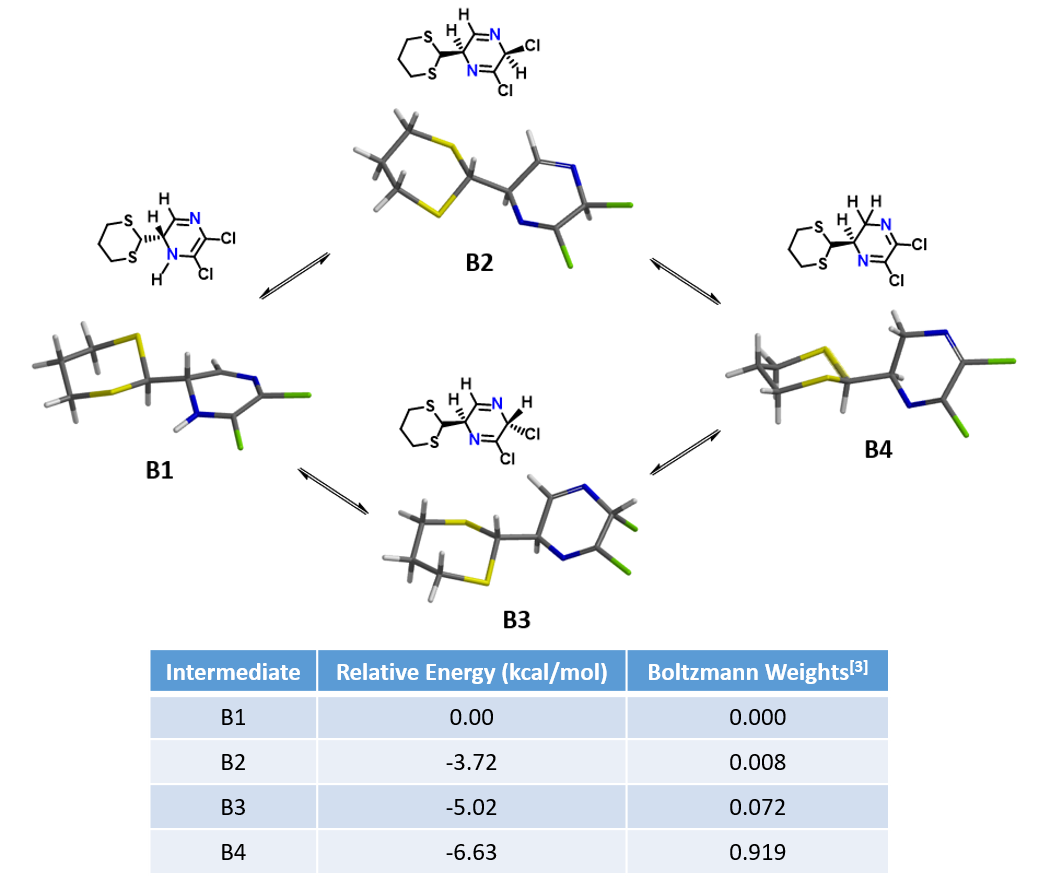

图6. B的四种可能结构及其对应的相对能量和所占比例

反应能量变化曲线计算验证反应机理

我们模拟异构体B3消除HCl芳构化过程的能量变化曲线（图7）。6位C-H之间的距离从1.096 Å到相互远离的3.096 Å，步长0.2 Å。加水淬灭反应的同时会生成氢氧根离子，它可以与C6位的酸性氢原子相互作用形成水分子。同时，处于同侧C3位假直立键的氯原子与这个水分子相互作用，最终以协同的方式离去。在HCl消除的同时，C3和C6两个碳原子由sp³杂化变为sp²杂化，分子芳构化生成化合物C。计算结果显示该过程能量快速下降，不需要克服任何能垒，表明HCl的消除应该可以顺利发生且非常快速。

图7. 异构体B3在氢氧负离子作用下消除HCl的反应能量变化曲线

对于中间体B2，离去的氯原子处于假平伏键，且与C6位假直立键的氢原子分布在环的两侧，不存在上述的协同作用。计算反应能量变化曲线没有得到消除产物，表明该过程存在较高的反应能垒，因此，通过该途径消除的可能性较低（图8）。

图8. 异构体B2在氢氧负离子作用下消除HCl的反应能量变化曲线

总结一下，通过LUMO和LUMO map的分析，我们揭示了2,3-二氯吡嗪各个碳原子发生亲核取代反应的活性差异原因，以及与不同类型亲核试剂反应时的位点选择性。之后，进一步利用反应能量变化曲线计算，验证了HCl消除芳构化的反应机理，合理的解释了C3位的氯原子离去的原因。

小试牛刀

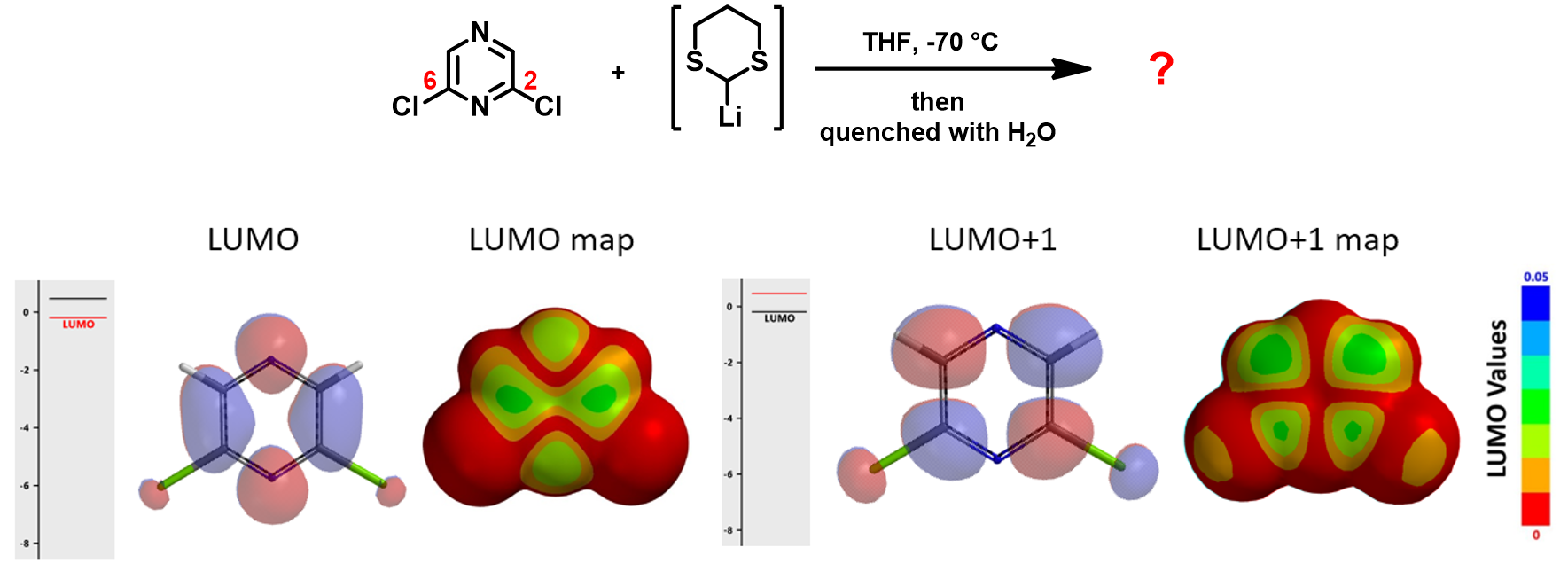
如图9所示，同样的反应条件下，将底物换成2,6-二氯吡嗪，会得到什么产物呢？我们给大家提供了2,6-二氯吡嗪的LUMO/LUMO+1 和LUMO/LUMO+1 map。你能试着按上文的思路，给出一个合理的预测吗？

图9. 2,6-二氯吡嗪的LUMO/LUMO map（左）及LUMO+1/LUMO+1 map（右）

温馨小提示：

下一章的魔法小课堂将为大家介绍QM在辅助理解碳酸二甲酯与不同亲核试剂反应结果方面的应用，敬请期待！

References:

[1] Torr, J.E.; Large, J.M.; Horton, P.N.; Hursthouse ,M.B.; McDonald, E. Tetrahedron Lett.2006, 47, 31.

[2] Joule, J.A. & Mills, K. Heterocyclic Chemistry 5th Ed. Chichester, West Sussex, UK: Blackwell Publishing Ltd., 2010, 256.

[3] 玻尔兹曼分布函数描述了在热平衡下，分子按能量高低的概率分布。

本文由董立亭、周正权、赖光华、潘东、石谷沁、卫小文编撰。