如果一个化合物中一个官能团因其结构改变成为含另一种官能团的异构体，并且两者能够迅速地相互转换，成为处在动态平衡中的两种异构体，这种现象就称为互变异构现象，这两种异构体称为互变异构体。一个分子的互变异构体通常具有不同的分子指纹、疏水性、静电性质、酸性，甚至其空间构型^[1]。研究比较多的互变异构体之一是2-羟基吡啶和2-吡啶酮，这两种互变异构体之间的平衡受溶剂性质影响很大，不同溶剂中的平衡常数如图1所示^[2]。直观上并不容易理解，那么QM是否能帮助我们解释这些现象呢？

图1. 2-羟基吡啶和2-吡啶酮互变异构体平衡中的溶剂效应

2-羟基吡啶与2-吡啶酮的互变异构化

首先，从DFT计算（图2，计算级别：ωB97X-V/6-311+G(2df,2p)^[3]）结果可知，2-羟基吡啶碳-碳距离为1.381 Å，1.396 Å，1.380 Å，1.397 Å，表明为芳香共振结构。而在2-吡啶酮中，碳与碳的距离长短交替为：1.354 Å，1.427 Å，1.357 Å，1.449 Å，这更匹配碳碳单键和双键的定义。2-吡啶酮中的碳氮距离为1.363 Å和1.391 Å，比2-羟基吡啶中的碳氮距离（1.340 Å，1.321 Å）长得多，与碳氮单键键长更一致。这些键距数据表明2-吡啶酮不具有芳香性。在环己烷（25℃）中，2-羟基吡啶和2-吡啶酮之间的实验平衡常数（K_eq）为1.7，表明能量差异相对较小，约为0.32 kcal/mol，2-吡啶酮略占优势。

图2. 2-羟基吡啶和2-吡啶酮的DFT计算

((ωB97X-V/6-311+G(2df,2p)，C-PCM模型，介电常数2.02，环己烷)

为理解这两种互变异构体在环己烷和氯仿溶液中平衡常数的变化，我们计算考察二者偶极矩（图 3）。

图3. 2-羟基吡啶和2-吡啶酮之间的平衡及其偶极矩计算

从计算结果可知，2-吡啶酮偶极矩^[4]在环己烷和氯仿中分别为5.29和5.97 Debye，高于2-羟基吡啶，分别为1.65和1.83 Debye，2-吡啶酮在氯仿中比2-羟基吡啶相对更稳定，介电常数高于在环己烷中，这就解释了实验平衡常数K_eq从1.7上升到6.0的现象。偶极矩矢量的位置、方向和大小，其中+号是指偶极矩的正端，与互变异构体上的电荷分布和电荷分离程度相关。偶极矩差异也可以视化，如图4所示，原子自然电荷与静电势图结合可以很显著的看出，2-吡啶酮比2-羟基吡啶拥有更大程度的电荷分离。

图4. 2-羟基吡啶和2-吡啶酮偶极矩/自然电荷/静电势结合图

当溶剂从氯仿变为乙腈和水，实验平衡常数K_eq的变化超出基于溶剂介电常数变化差异的预期值。如何解释这些情况？我们决定进一步考察2-羟基吡啶/2-吡啶酮在水存在下的互变异构作用。

图5. 2-羟基吡啶和2-吡啶酮之间的平衡及其偶极矩计算

我们需要进一步理解：

a.溶剂化效应将如何影响2-羟基-吡啶与2-吡啶酮之间互变异构的能量壁垒？

b.溶剂水如何作用于2-吡啶酮，改变其相对能量，将互变异构平衡从羟基转移到酮的形式？

图6.非溶剂化2-羟基吡啶与2-吡啶酮内禀反应坐标（IRC）示意图

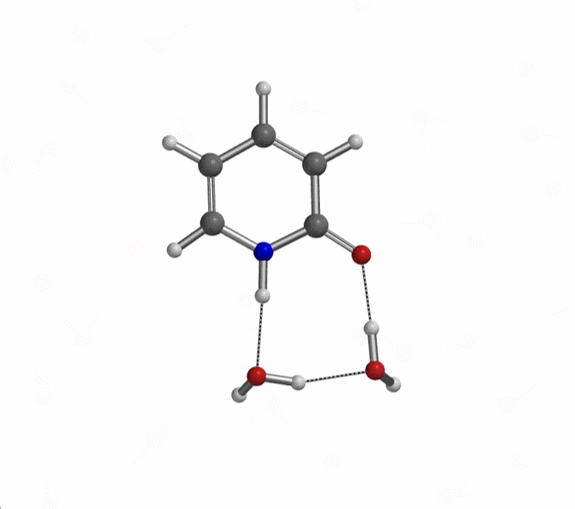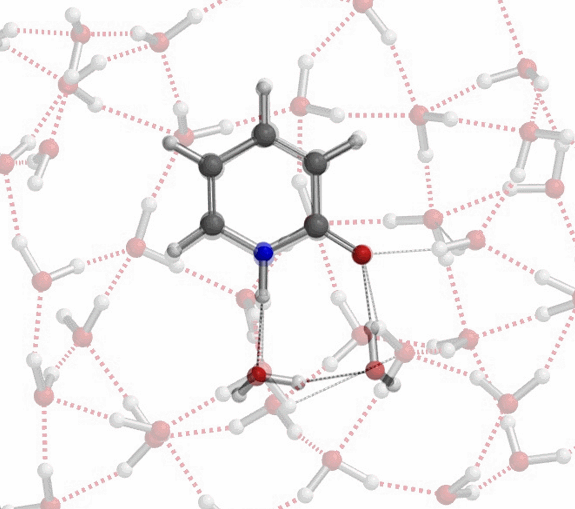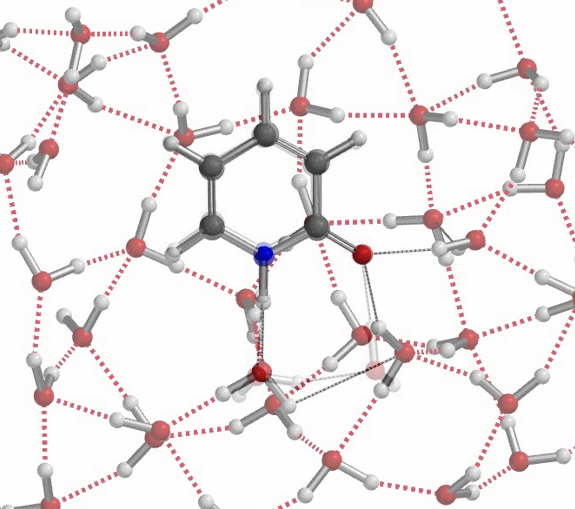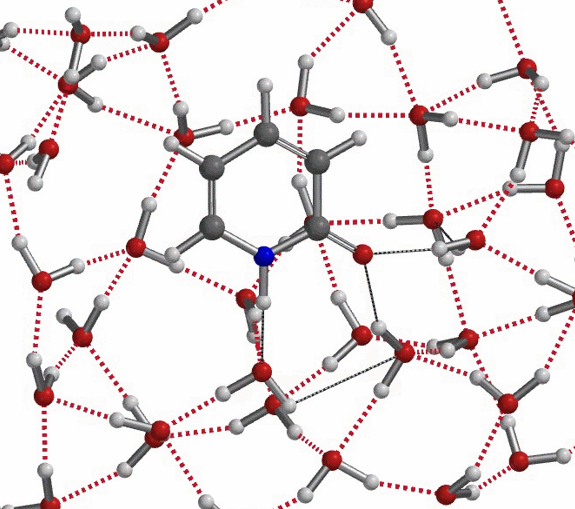
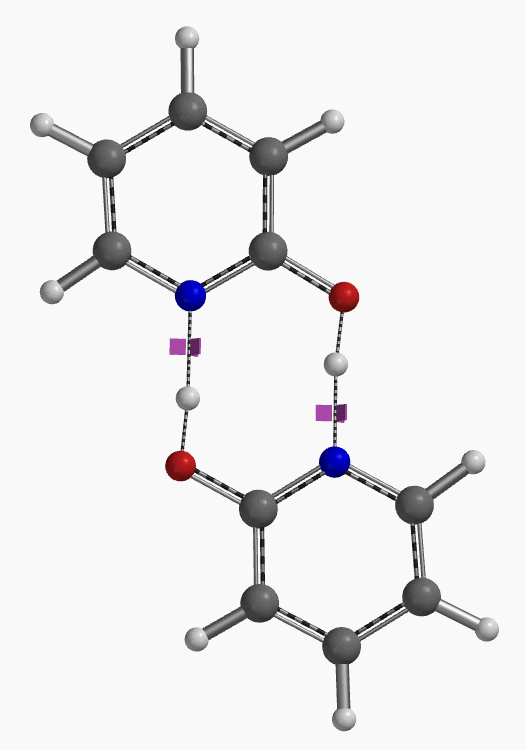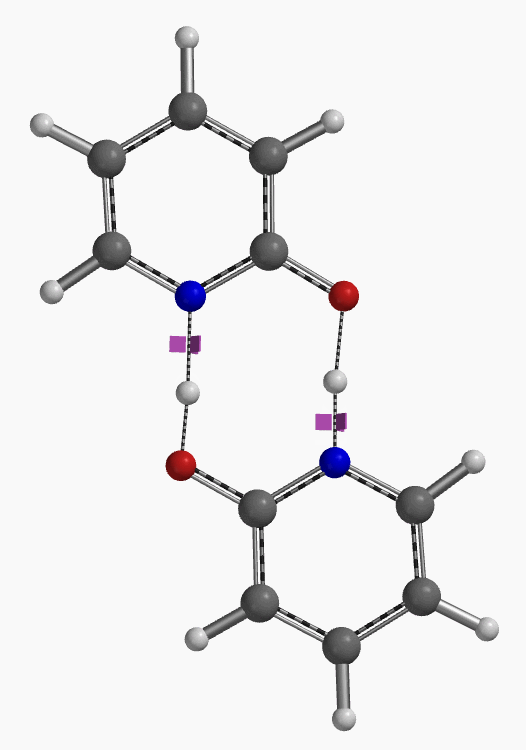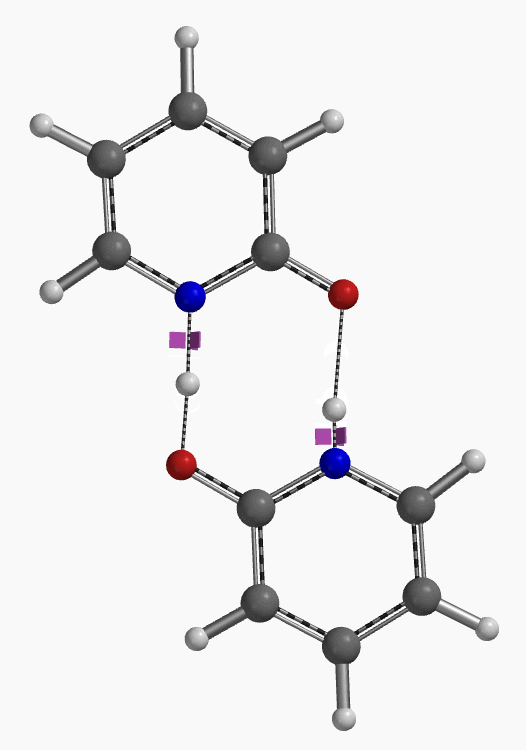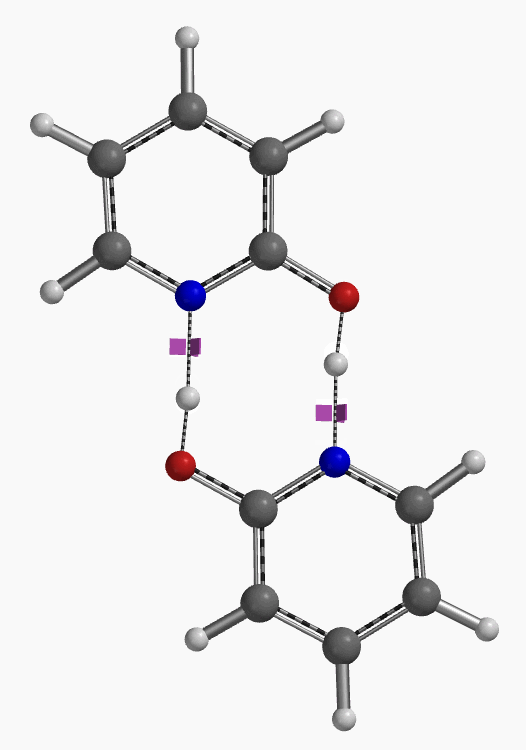
通过DFT过渡态计算^[5]及内禀反应坐标示意图（图 6）可知，对于2-羟基吡啶和2-吡啶酮之间的非溶剂化平衡，能量壁垒为38.21/38.24 kcal/mol，这是一个极高的能量屏障。当2-吡啶酮N-H和C=O部分存在单个水分子桥接时，该值显著降低至12.12/16.74 kcal/mol（图 7）。进一步变更为双分子水桥接形式的能量壁垒约为13.17/17.51 kcal/mol（图 8）。水分子的存在极大降低了互变异构体形式之间的互变异构屏障，同时2-吡啶酮水复合物比2-羟基吡啶更稳定。

图7. 2-羟基吡啶和2-吡啶酮一水合物之间的内禀反应坐标（IRC）示意图

图8. 2-羟基吡啶和2-吡啶酮二水合物之间的内禀反应坐标（IRC）示意图

水通过形成氢键与2-吡啶酮发生溶剂化作用，并将互变异构平衡从羟基转移至酮形式。微溶剂化模型计算表明，溶剂化是一个能量上非常有利的过程，结合第一个和第二个水分子所需能量分别为-5.08和-6.69 kcal/mol（图 9）。2-羟基吡啶和2-吡啶酮与一个或两个水分子的水合配合物的存在以及水催化达到平衡得到了Molecular Beam Fourier Transform Microwave spectroscopy的实验支持^[6]。

图9. 2-吡啶酮和水的微溶剂化模型

上述微溶剂化模型半定量地为我们提供了一个图景，阐明如何在氢键作用下，互变异构体的平衡常数K_eq从6（氯仿）上升到910（水）、实现超过150倍的变化，同时这种变化也体现出极性非质子溶剂或者少量的水会使事情复杂化。更现实的模型应该在2-吡啶酮周围有一簇水分子，如图10所示，以便更精确地评估溶剂化中的能量变化。

图10.水簇模型。很可能在溶剂化复合物中有两个以上的水分子

对于不存在水/质子溶剂的平衡，我们的计算显示了协同双质子转移。有趣的是，计算的过渡态（有且只有一个iFreq，889 cm^-1）表明存在异步过程，N-H键距离为1.433 Å vs 1.206 Å，O-H键距离为1.283 Å vs 1.089 Å（图 11）^[7]。

图11.不存在水/质子溶剂时的过渡态和IRC平衡

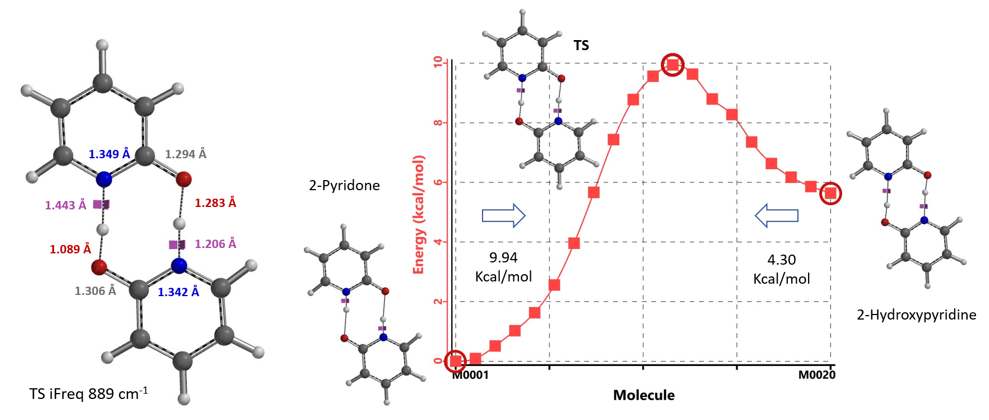
DFT分析帮助我们理解为什么2-羟基吡啶和2-吡啶酮的K_eq具有高度溶剂依赖性，以及为什么少量水使极性非质子溶剂中的分析变得复杂。

4-氯-10-羟基-1,7-二氮杂菲的互变异构

4-氯-10-羟基-1,7-二氮杂菲与4-吡啶酮结构相关，表现出独特的互变异构特征（图 12）。在九十年代，Katritzky等人曾对该互变异构进行了研究^{[8, 9, 10]}，发现该互变异构对溶剂极性变化不太敏感，这值得我们进一步通过QM分析再审视。我们通过“Generate Tautomers”工具^[11]将互变异构体C添加到之前报告的两个列表A和B中，以供考查。

图12. 4-氯-10-羟基-1,7-二氮杂菲互变异构体

从4-氯-10-羟基-1,7-二氮杂菲的DFT电子密度等值线图可知，烯醇型B和酮型C中存在较强的分子内氢键结合。而在吡啶型A中，羰基O与吡啶N之间的电子密度要小得多。红外光谱显示在CCl₄或CHCl₃中，在2300–3500 cm^-1有广泛的吸收，表明氢键结合较强，互变异构体A是少量的构型^[8]。

图13. 4-氯-10-羟基-1,7-二氮杂菲互变异构体的电子密度等值线图A,B,C

QM计算得到4-氯-10-羟基-1,7-二氮杂菲A，B，C互变异构体¹³C NMR位移值，与实验数据^[10]结合进行DP4^[12]分析（图 14），其评分分别为0%，100%，0%，DFT计算的互变异构体相对能量分别为6.33，0.00，5.83 kcal/mol，有力地支持了分子内氢键结合烯醇B是主要的互变异构体。在两种酮形式中，具有分子内氢键的互变异构体C的能量低于互变异构体A。

图14. 4-氯-10-羟基-1,7-二氮杂菲的13C NMR 实测值、计算值

及A,B,C互变异构体的DP4评分

从图15可知，计算平衡的能量壁垒从酮C至烯醇B约为0.50 kcal/mol，反向为6.31 kcal/mol，表明平衡将在室温下快速进行。

图15.互变异构体B和C间的内禀反应坐标示意图

值得注意的是，不同于2-羟基吡啶酮和2-吡啶酮之间的互变异构体，具有强分子内氢键的互变异构体通常对溶剂极性变化不太敏感^[10]。

总结

在对待可能存在两种或两种以上不同互变异构体平衡的杂环化合物时，互变异构体的鉴定尤其重要。优势构型的鉴别可能并不直观明显，精确的实验测定和互变异构平衡的QM分析是一个重大的挑战。在药物化学设计中，互变异构体的存在使复杂性和不确定性成倍增加。结合口袋中的局部带电或极性基团可使互变异构体比率发生偏移，并在游离溶液中与高能互变异构体结合。所有这些都使得互变异构容易被忽略，但值得我们去考察^[1]。QM可能无法精确定量溶液中互变异构体之间的微小能量差异，但其在区分差异 ≥10 kcal/mol的互变异构体方面高度可靠。通过蛋白结合补偿10 kcal/mol不太可能达到适用于临床开发的低纳摩尔强效候选物，而几kcal/mol的互变异构能差异可能更容易补偿。蛋白与能量差较多的异构体结合情况可以通过片段分子轨道计算进一步分析^{[13, 14, 15]}。用于分析化合物互变异构的QM工具易于操作，我们应将其应用常规化助力分子设计和优化工作。

小试牛刀

γ-羟丁烯内酯是在Palauolide^[16], Cacospongionolide A, Dysidiolide, Manoalide^[17]等多种生物活性海洋天然产物中发现的重要母核结构等，并被认为是这类化合物的关键药效团，具有多样的生物学特性。

图16.含有γ-羟基丁烯内酯基团的一些天然产物

纵观这些重要天然产物的结构，我们不禁要问：

a.为什么羟基总是在丁烯内酯的多取代一侧？

b.根据以下所示三种互变异构体形式的相对能量，γ-羟基-丁烯内酯是否会平衡至其他互变异构体形式？

图17.潜在的γ-羟基丁烯内酯互变异构作用

本文由董立亭、王秋月、卫小文编撰。

参考文献：

[1] Y. C. Martin J. Comput. Aided Mol. Des.,2009,23, 693.

[2] E.V. Anslyn, D.A. Dougherty (2006) Modern Physical Organic Chemistry. New York, NY, USA: University Science Books; page 155.

[3] For DFT calculation of tautomers, ωB97X-V/6-311+G(2df,2p) is a more accurate model than the standard ωB97X-D/6-31G* one we routinely used for other QM calculations.

[4]Spartan'20 Tutorial and User's Guide(2020). Irvine, CA, USA: Wavefunction, Inc. page 50.

[5] Transition States calculated for tautomeric equilibration between 2-hydroxypyridine and 2-pyridone in the presence of zero, one, and two water molecules.

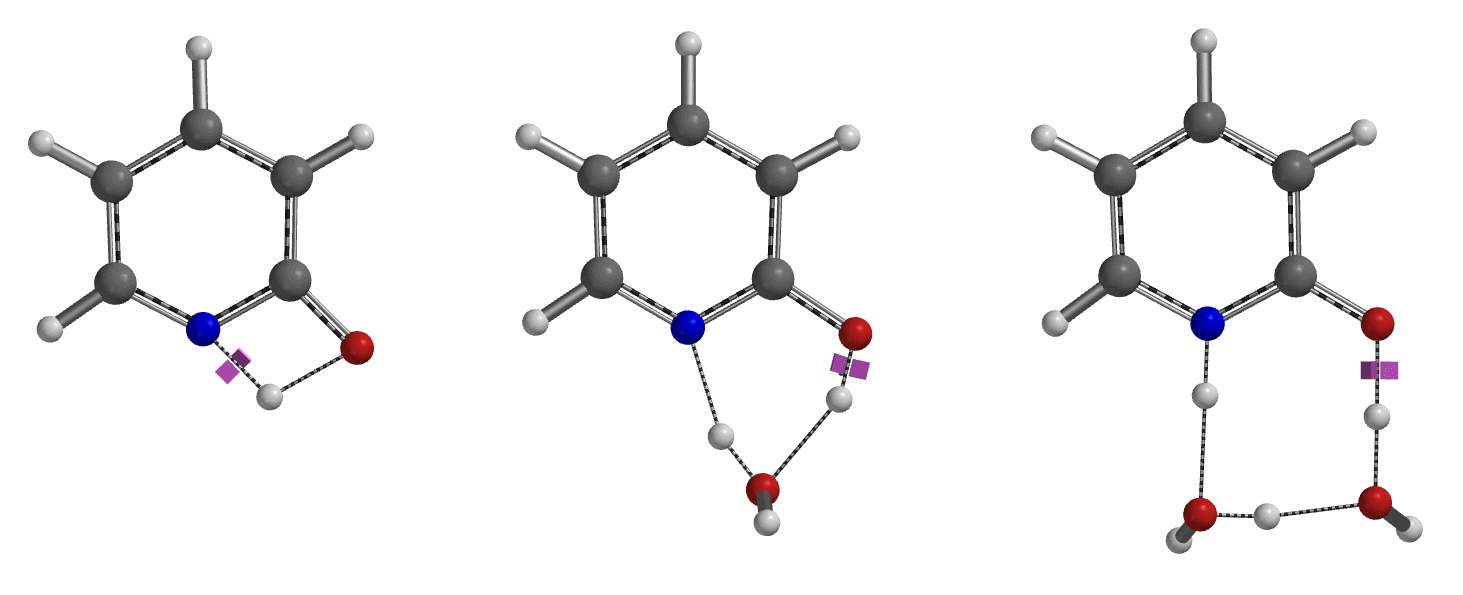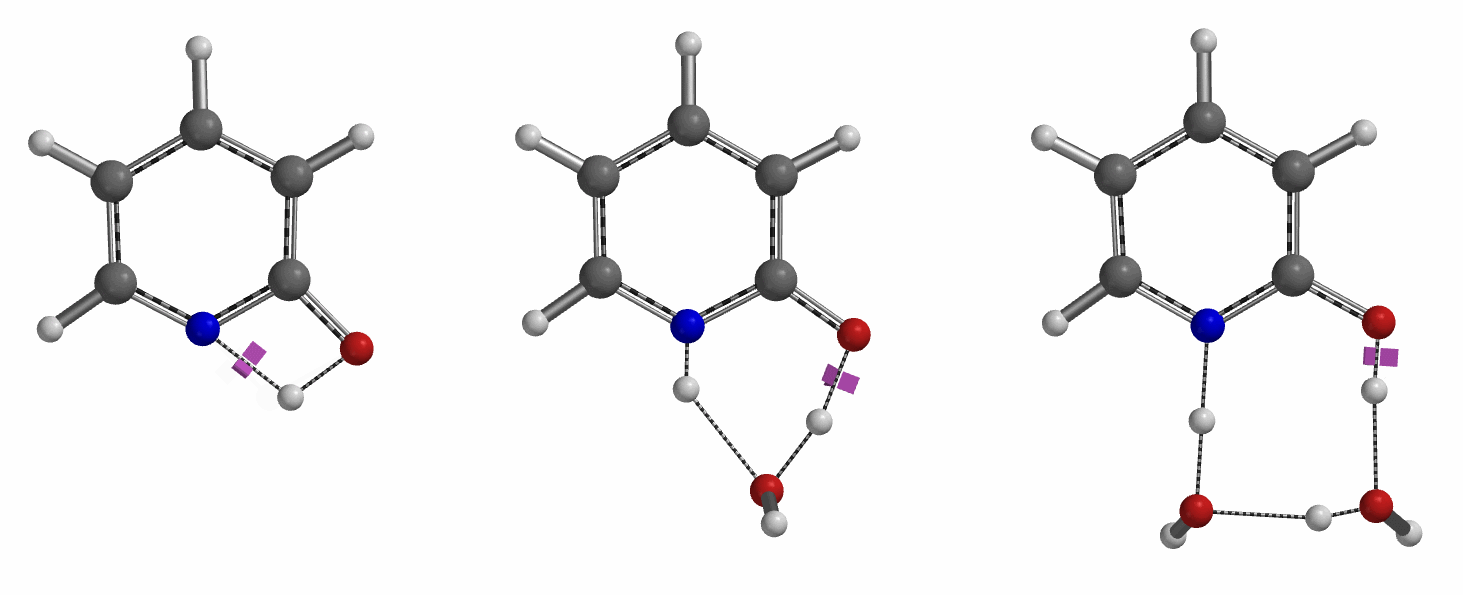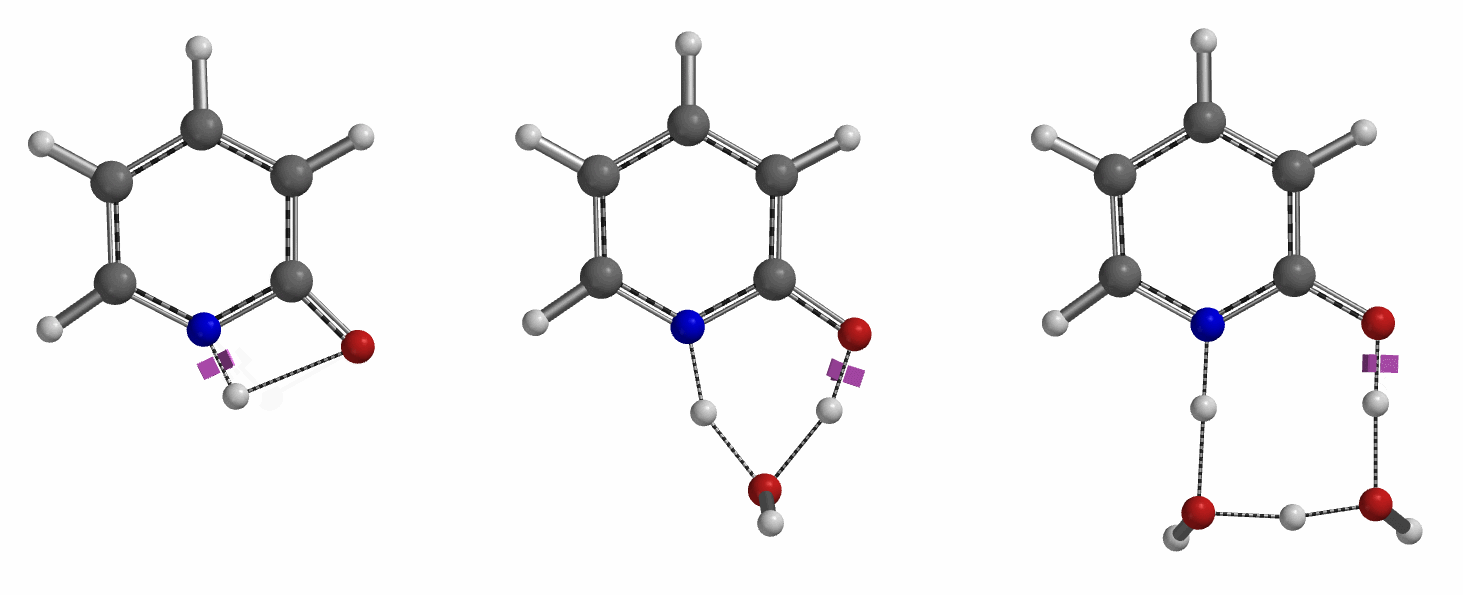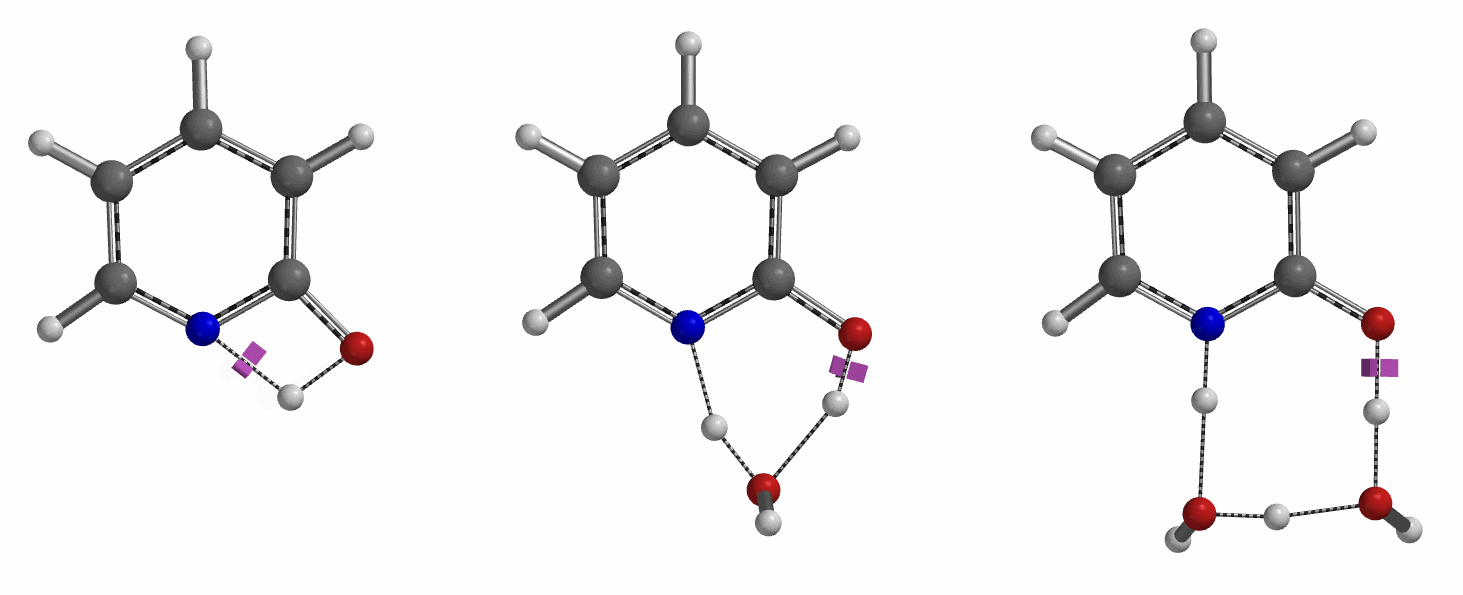
[6] S. Mata, V. Cortijo, W. Caminati, J. L. Alonso, M. Eugenia Sanz, J. C. López, S. Blanco J. Phys. Chem. A2010,114, 11393.

[7] A. Fu, H. L. Li, D. M. Du, Z. Y. Zhou J. Phys. Chem. A2005,109, 1468. This paper studied the 2-pyridone dimer tautomer equilibration with B3LYP and BH-LYP hybrid density functional methods at the 6-311++G (2d, 2p) basis set level. Results suggest the process to beconcertedandsynchronous. E. Torres, G. A. DiLabio, J. Phys. Chem. Lett.2012,3, 1738 noted that B3LYP is not able to reliably model systems in which noncovalent interactions are important (hydrogen bonding, π-stacking, etc.).

[8] I. Shcherbakova, J. Elguero, A. R. Katritzky, Advances in Heterocyclic Chemistry, 2000, 51.

[9] A. R. Katritzky, M. Karelson, P. A. Harris, Heterocycles1991,32, 329.

[10] A.R. Katritzky, I. Ghiviriga, P. Leeming, F. Soti Magnetic Resonance in Chemistry,1996,34, 518.

[11] Tautomer Generators

a.Spartan'20 Tutorial and User's Guide(2020). Irvine, CA, USA: Wavefunction, Inc. page 269. Spartan’20 tautomer generating tool is limited to tautomers involving nitrogen, oxygen, phosphorus, and sulfur. Tautomers involving carbon have intentionally been excluded. And as such Spartan’20 “Generate Tautomer” does not alert the possibility of the keto form as shown below

Figure 18. Spartan’20 Tautomer Generation Tool

b. D. K. Dhaked, W.-D. Ihlenfeldt, H. Patel, V. Delannée, M. C. Nicklaus J. Chem. Inf. Model.2020,60, 1253. Tautomerizer is a more thorough tautomer generator. This web tool is available at https://cactus.nci.nih.gov/tautomerizer/

[12] S. G. Smith, J. M. Goodman J. Am. Chem. Soc,2020,132, 12946. T.-H. Duong, M. A. Beniddir, J. Boustie, K.-P.-P. Nguyen, W. Chavasiri, G. Bernadat, P. Le Pogam Molecules,2019,24, 1527.

[13] M. Wieder, J. Fass, J. D. Chodera Chem. Sci.2021,12, 11364.

[14] H. Brandstetter. F. Grams, D. Glitz, A. Lang, R. Huber. W. Bode, H-W. Krell, R. A. Engh J. Biol. Chem.2001,276, 17405. Enol form of RO200-1770 is 17.14 kcal/mol higher in energy than the keto form.https://www.rcsb.org/structure/1jj9form

[15] For recent reviews on Fragment Molecular Orbital Analyses, see Alexander Heifetz editor Quantum Mechanics in Drug Discovery, 2020, Springer Science+Business Media, LLC, New York, NY 10004, U.S.A. Guiding Medicinal Chemistry with Fragment Molecular Orbital (FMO) Method. pp. 37-48, Analyzing Interactions with the Fragment Molecular Orbital Method pp. 49-73.

[16] T. Mai, J. Toullec, S. Van Wynsberge, M. Besson, S. Soulet, S. Petek, E. Aliotti, M. Ekins, K. Hall, D. Erpenbeck, D. Lecchini, M. A. Beniddir, D. Saulnier, C. Debitus Fish. Aquatic Sci.2019,22, 30.

[17] S Tilvi, S Khan, M.S Majik Current Org. Chem.2019,23, 2436.