1,2,3-三氮唑是药物化学中的常见骨架，具有该结构的化合物往往呈现广泛的生物活性。1,4-取代的1,2,3-三氮唑作为基本的药效团，具有多功能性 (图1)：它可以作为特定功能基团的生物等效替代物；作为分子支架，它调节其他药效基团维持活性构象；可以作为药效基团原件的链接单元；基于其对蛋白酶的稳定性，发挥拟肽作用；在多种情况下作为连接子发挥作用，比如作为PROTACS的连接子；药物载体的连接子；靶向结合物或者探针的连接子等等^[1]。

Click-Chemistry-mediated rapid synthesis of bispecific molecules for inducing protein degradation.

Click-Chemistry-mediated conjugation of a nonspecific antiviral Sapogenin with a HIV fusion inhibitor.

图1 1,2,3-三氮唑骨架在药物合成中应用示例

1,2,3-三氮唑结构一般通过传统的[3+2]环加成反应，以及近些年由Sharpless教授提出的Click chemistry (图2) 构建。两种方法都需要叠氮化合物作为起始原料，而叠氮基为高活性官能团，常具有剧毒和易制爆的特性，因此，安全制备和使用叠氮化合物至关重要。

图2 1,2,3-三氮唑骨架构建示例

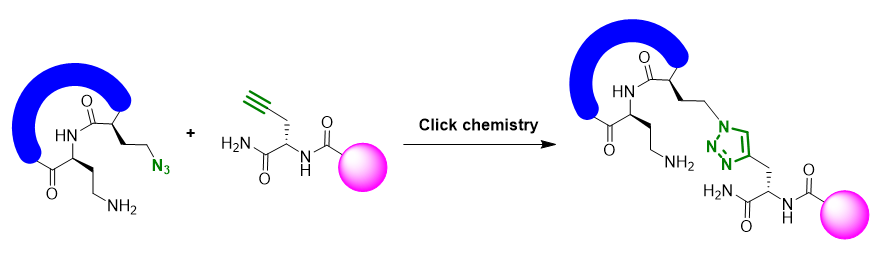
2019年，中科院上海有机所的董佳家和K. Barry Sharpless在Nature上发表了一种安全高效制备各种叠氮化合物的全新方法，并将其用于Click反应，构建含上千个分子的化合物库 (图3) ^[2]。

图3 发表在Nature上的叠氮转移反应

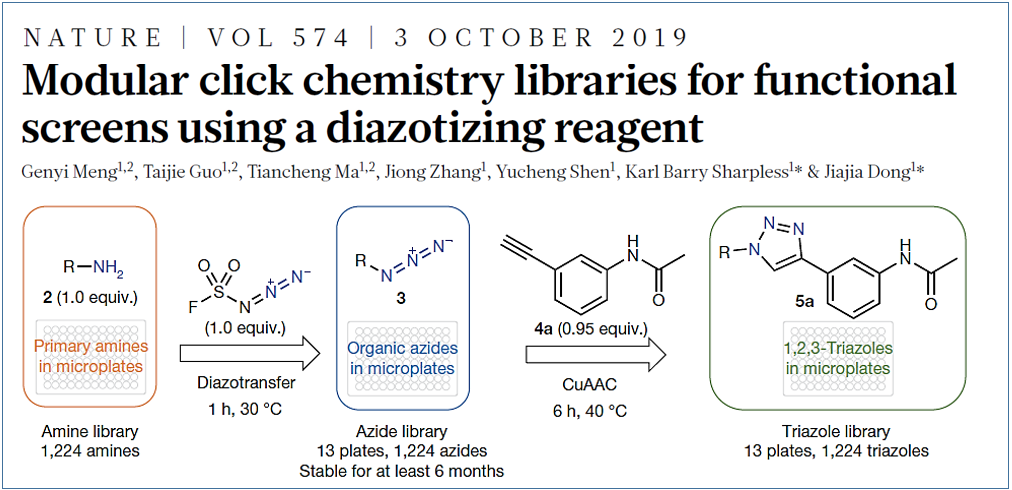
文中介绍的磺酰氟类化合物FSO₂N₃ (氟磺酰基叠氮)，表现出对于一级胺官能团异乎寻常的叠氮转移反应性。相对于传统的叠氮转移反应，该反应呈现诸多优点，如：室温即可以进行，反应底物是化学计量 (1:1)的，短时高效转化，方法适用于所有的一级胺，包括叔丁基伯胺都可以实现接近化学计量转化。本节QM小课堂，我们就该叠氮转移反应进行学习探讨。

反应机理探讨

我们知道，叠氮基团是两性基团，其亲电性使胺作为亲核试剂的叠氮转移反应成为可能。我们需要判断胺基的亲核进攻发生在叠氮的哪个氮原子上。(图4)

图4 磺酰氟叠氮LUMO示意图

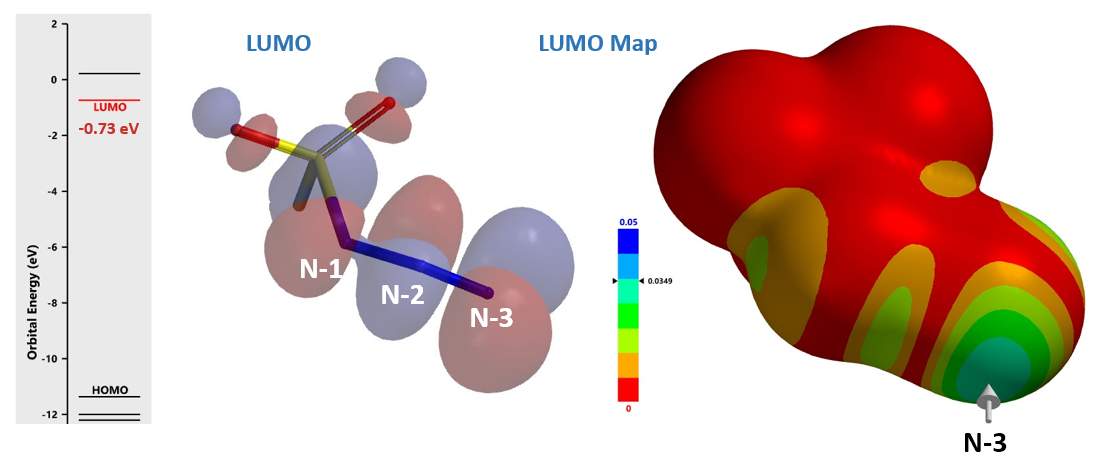
首先计算磺酰氟化合物的LUMO和LUMO map (第1章-亲核反应中LUMO计算的应用)，结果如图5所示。可以看到三个N原子的LUMO lobe N-3 > N-2 > N-1，而LUMO map清晰的显示出N-3比N-2更容易被接近，因此胺的亲核进攻更倾向于发生在N-3上。这与2014年发表在Tetrahedron Letters的《Mechanistic studies on the diazo transfer reaction》文章阐述的¹⁵N同位素标记实验的结果一致^[3]。

图5 磺酰氟叠氮的LUMO和LUMO map示意图

计算模型构建

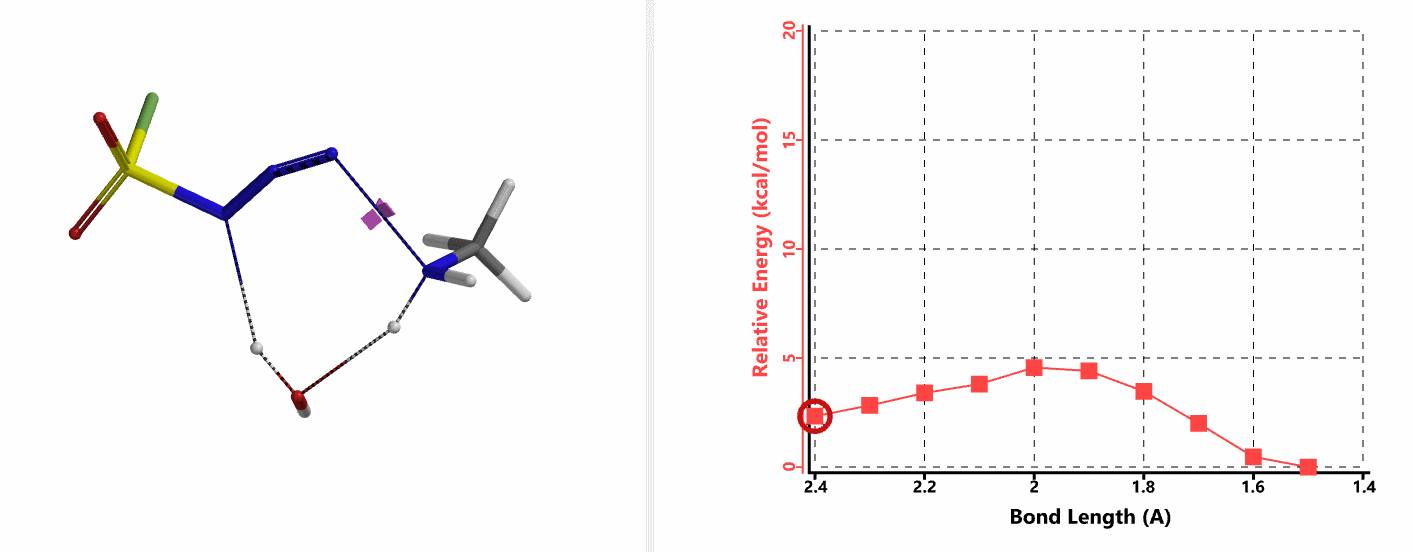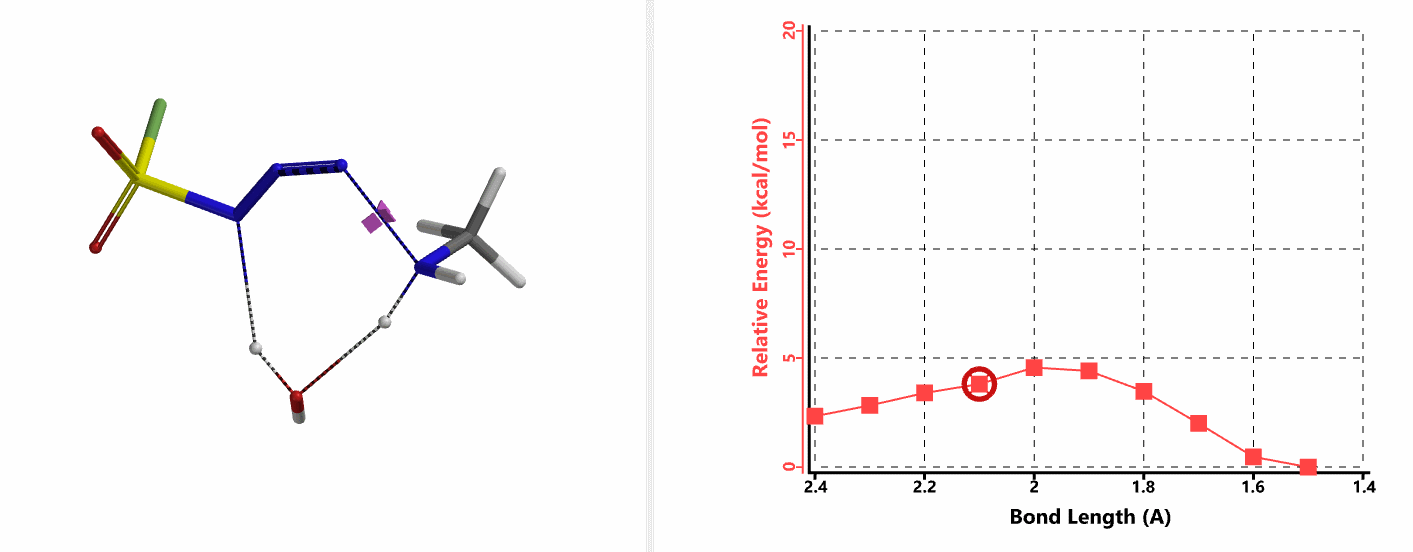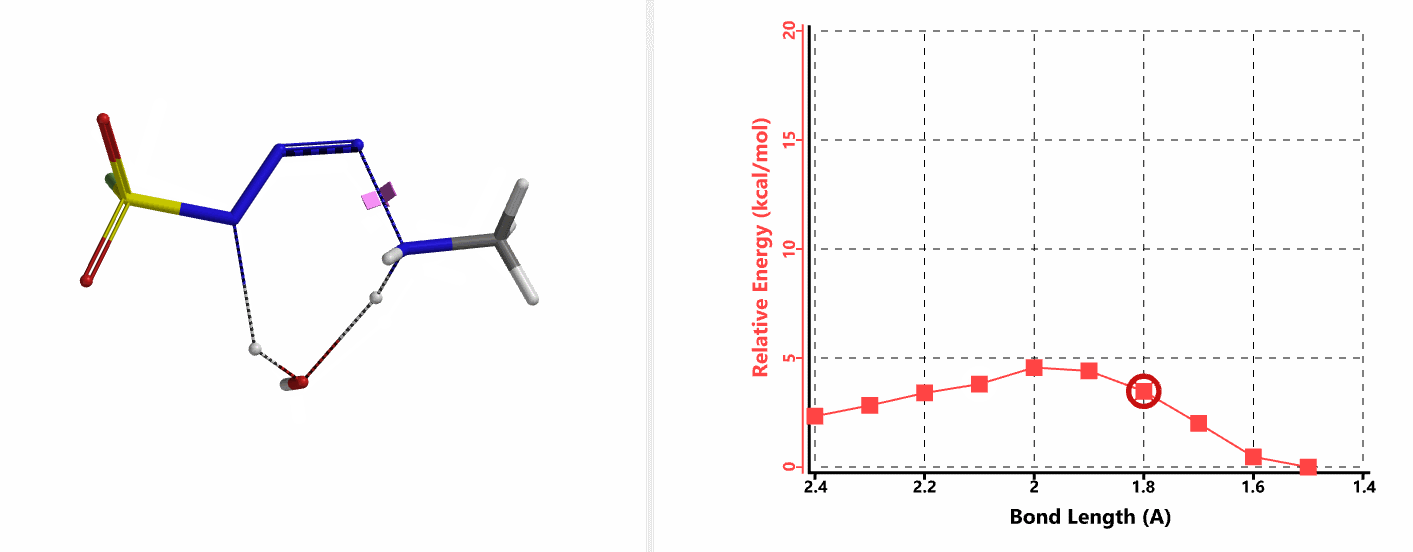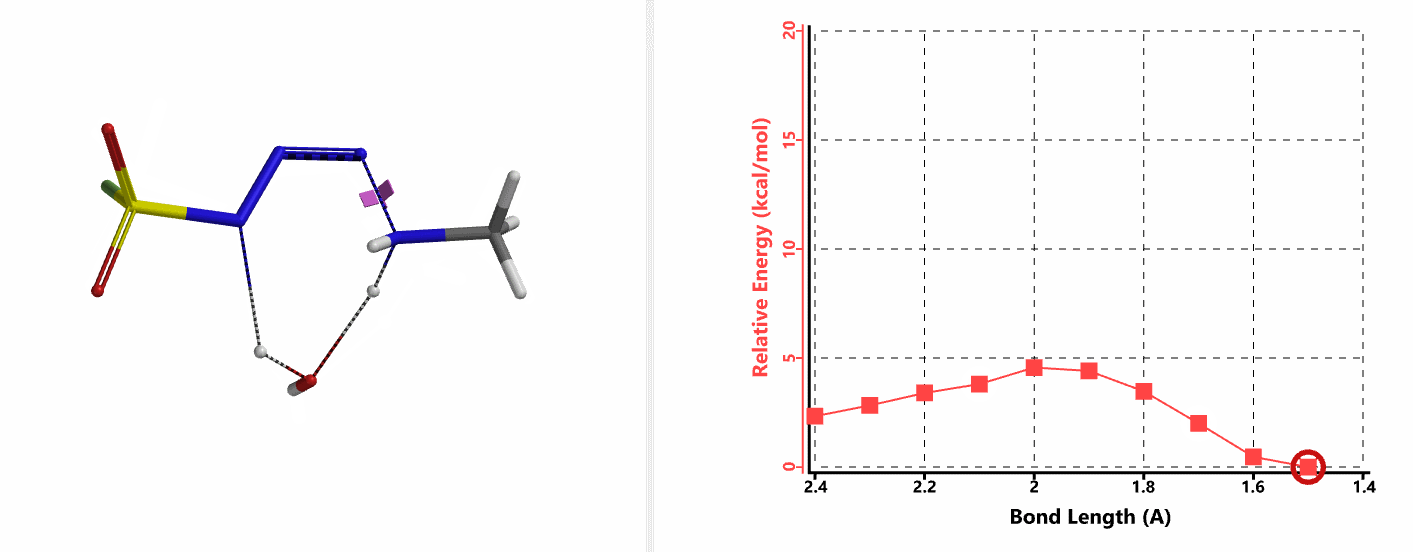
下面我们开始建立这个反应的计算模型。文章中的实验结果表明，水在这个叠氮转移反应中起到了一个关键的作用。在前期大量QM计算的基础上，我们认为胺基对叠氮加成是一个分步机理，而非协同机理 (图6)。首先胺进攻磺酰氟叠氮的N-3，接下来通过一个水分子参与的七元环过渡态，将一个氢原子转移到磺酰氟叠氮的N-1原子上。

图6 胺基对叠氮加成的可能机理

第一步计算

我们首先建立胺基进攻步骤的QM计算模型。经过前期计算分析，我们发现在这样的一个模型中，水的参与至关重要。胺的氮原子直接进攻磺酰氟叠氮的N-3原子，在没有水参与的情况下活化能大于20 kcal/mol。而在这个模型中加入一分子水，通过分子间氢键作用来同时稳定叠氮和胺，将N-N键的距离变化设定为从彼此间无相互作用的2.4 Å到足以形成共价键的距离1.5 Å，步长0.1 Å。计算结果表明水分子的参与能够大大降低该步的活化能，其能垒只有不足5 kcal/mol (图7-1)。

接下来，我们以N-N键成键后，最低能量的结构作为接下来氢原子转移步骤的起点，计算这一步的活化能。结果表明该步的活化能也只有约15 kcal/mol，在室温下同样能够顺利发生(图7-2) ^[4]。

图7-1 胺基进攻叠氮N-3原子的势能变化曲线

图7-2 经由水分子中继的氢原子转移的势能变化曲线

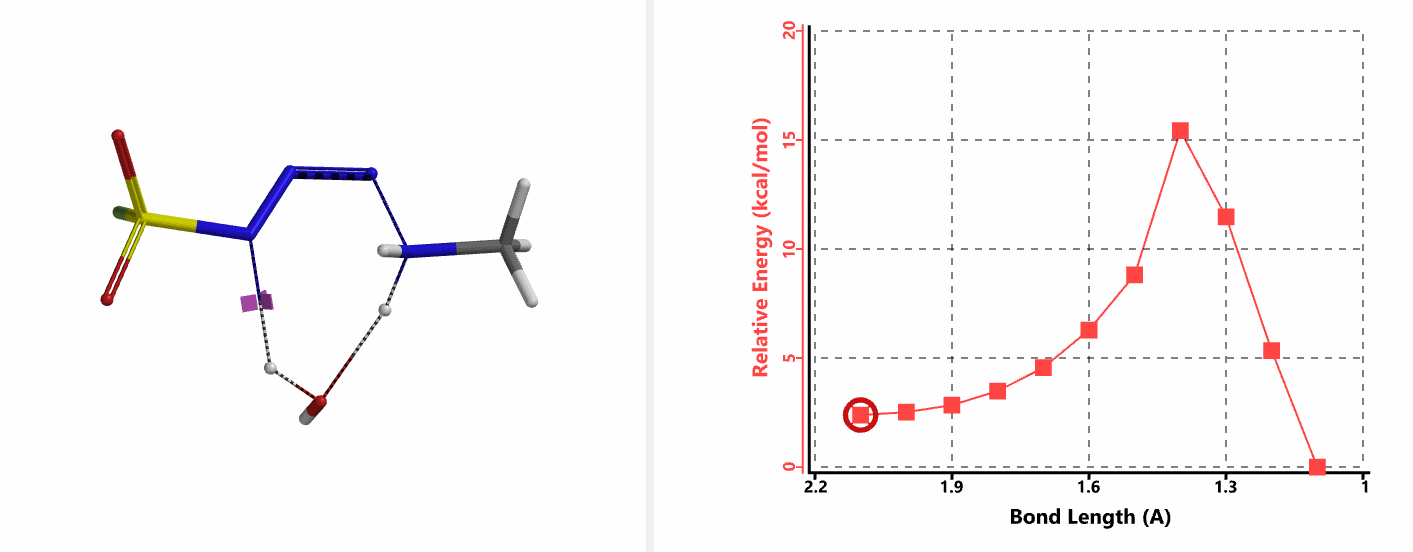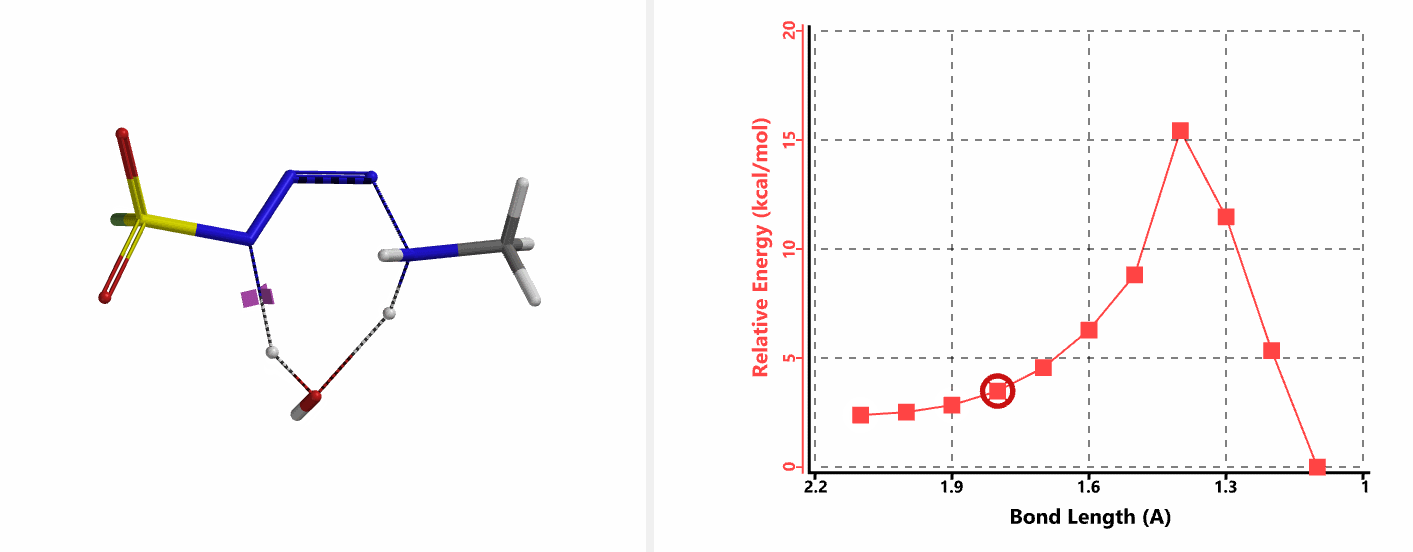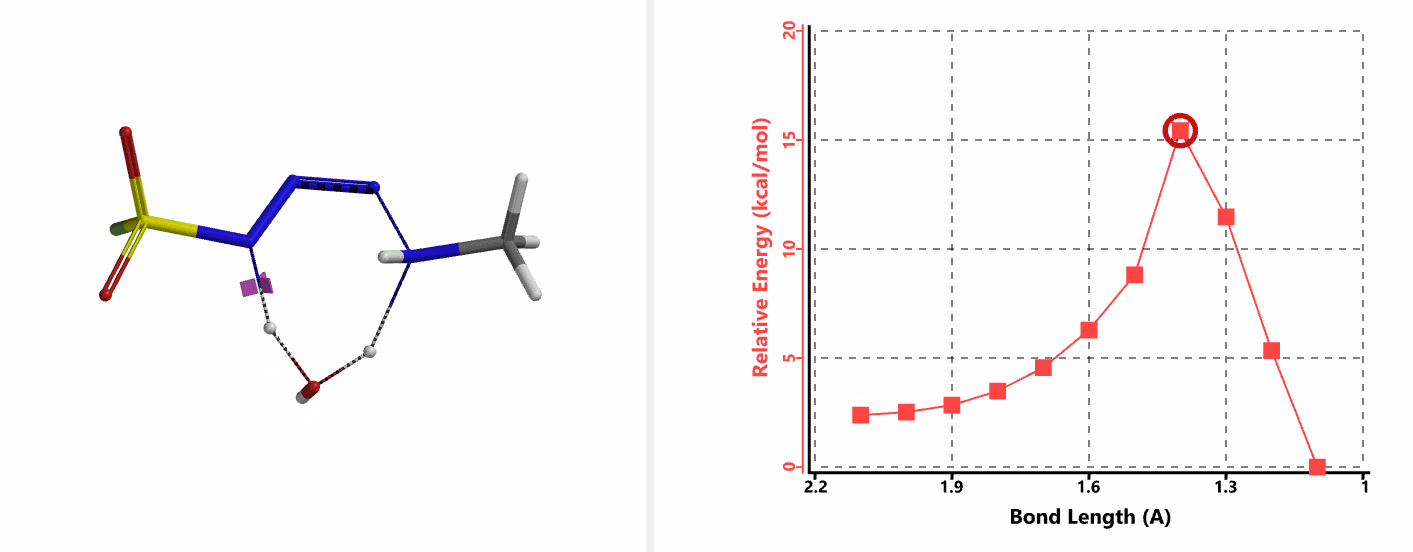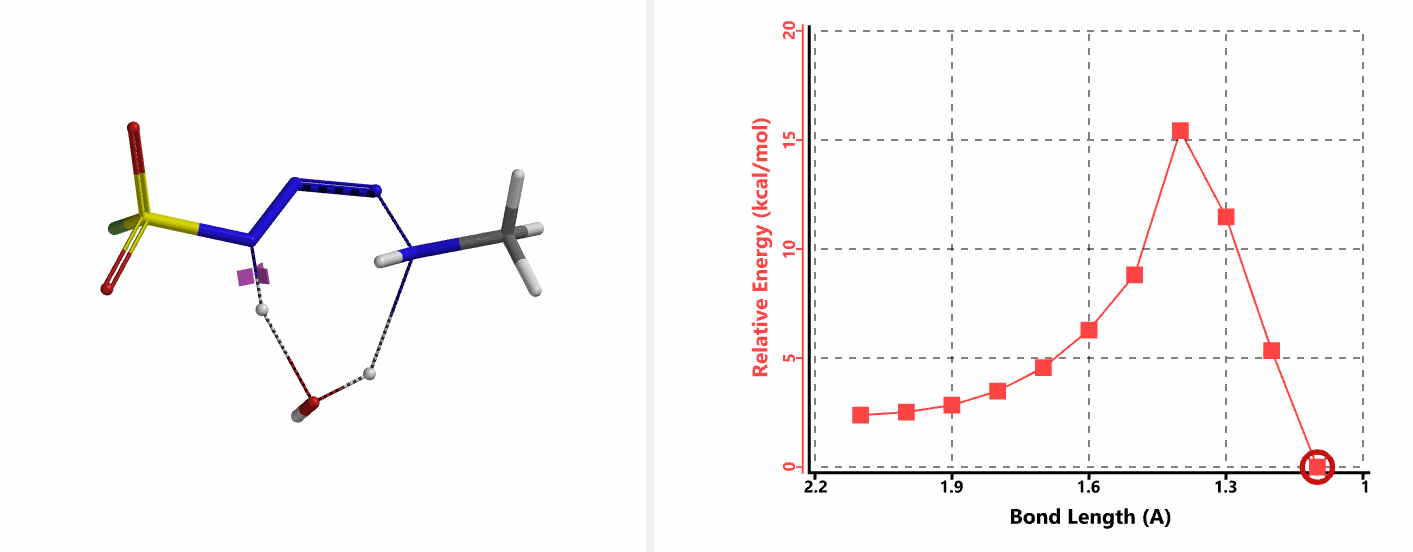
我们分别选取两个过程中能量最高点的结构，选择Transition State Geometry计算更加精确的过渡态能量，同时通过频率分析计算过渡态的虚频。结果表明两个过渡态结构均只有一个虚频，分别为136 cm^-1和1280 cm^-1，见图8。虚频相对于红外波谱中能观测到的各种分子振动的频率，并不是一个真实存在的频率。我们可以将其看做反应过渡态的结构，在向其能量最低状态运动的趋势，而将这个趋势近似为简谐运动时，所得到的频率即为虚频。当虚频只有一个时，我们可以认为在该点上的运动趋势仅有一组，即分别向着两个能量最低的状态运动 (起始物和生成物)，这意味着计算出的过渡态是合理的。

图8 胺基进攻叠氮N-3原子和氢原子转移步骤的过渡态结构及虚频

136 cm^-1 (左) 1280 cm^-1 (右)

第二步计算

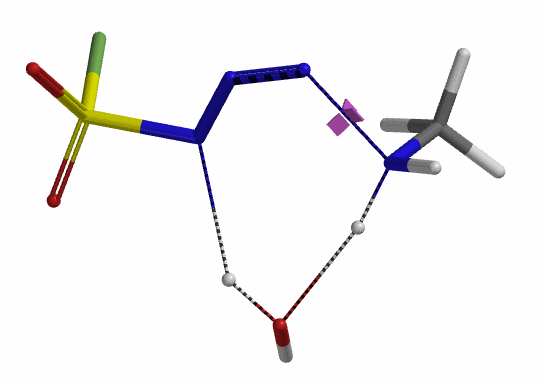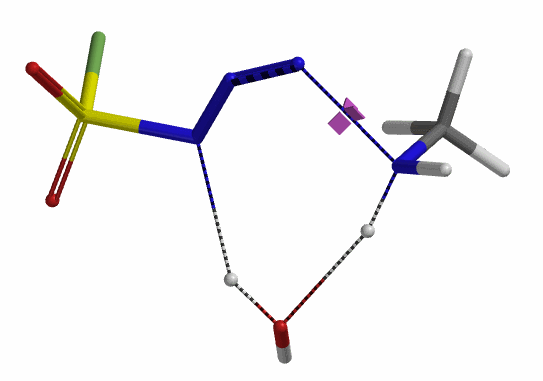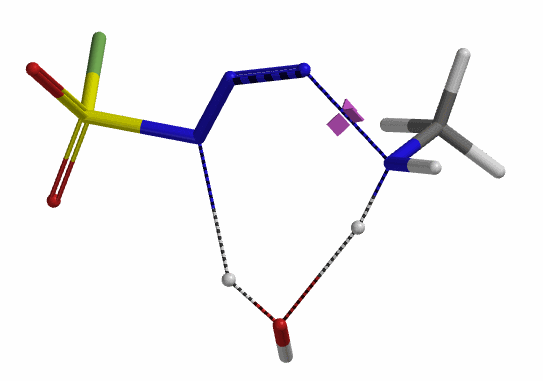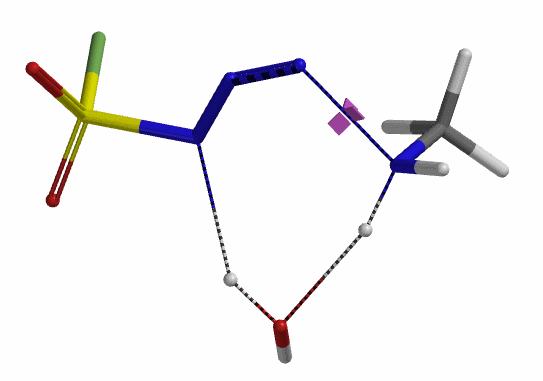
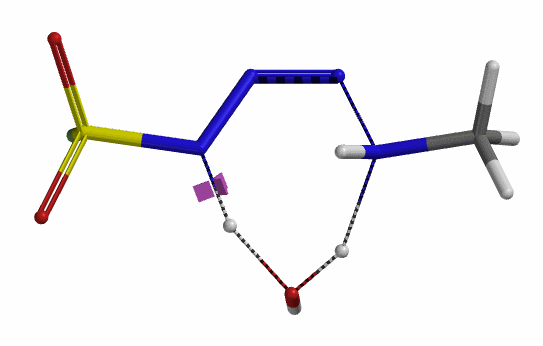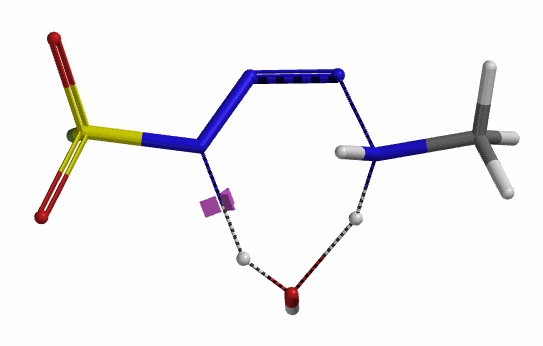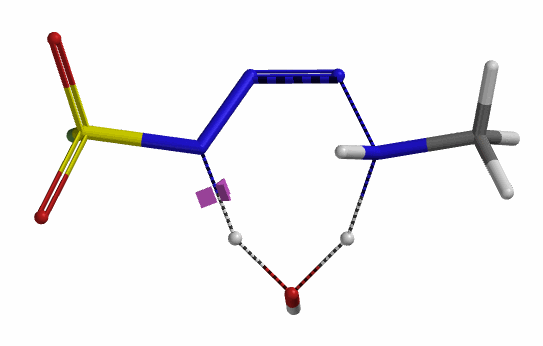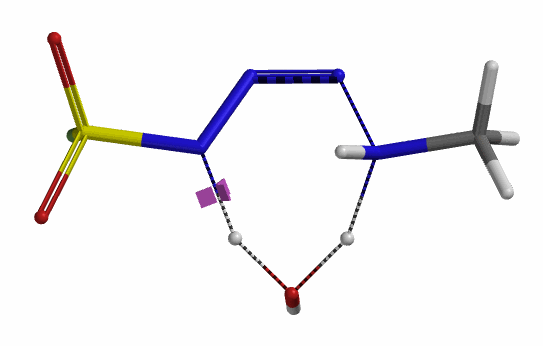
我们接下来计算第二步，即磺酰氟叠氮的N-N键断裂，以及第二个氢原子通过水分子，转移到磺酰氟叠氮N-1原子上的过程。经过计算，在没有水分子参与的时候，叠氮基团无法捕获到氢原子，导致反应无法发生。而在水分子参与其中时，这样一个过程的活化能约为20 kcal/mol。这一步具有整个反应历程中最高的能垒，说明这一步是整个反应的决速步 (Rate Limiting Step)。对过渡态结构进行频率分析同样只得到了一个虚频，为239 cm^-1，证实了这样一个过渡态的合理性 (图9)。

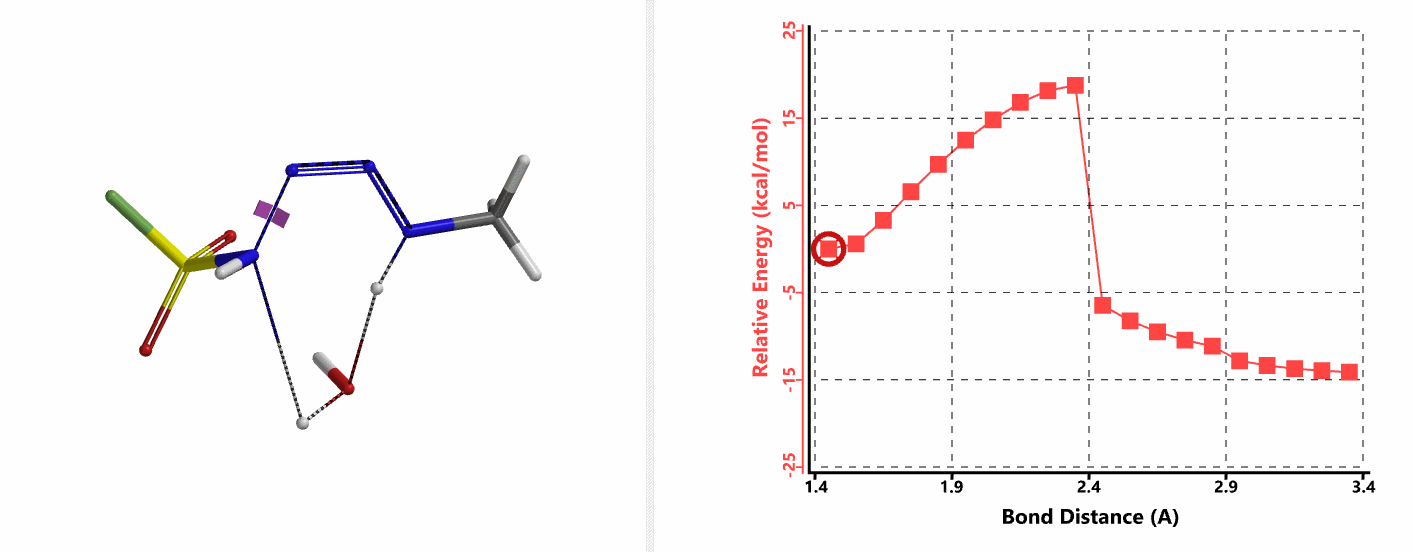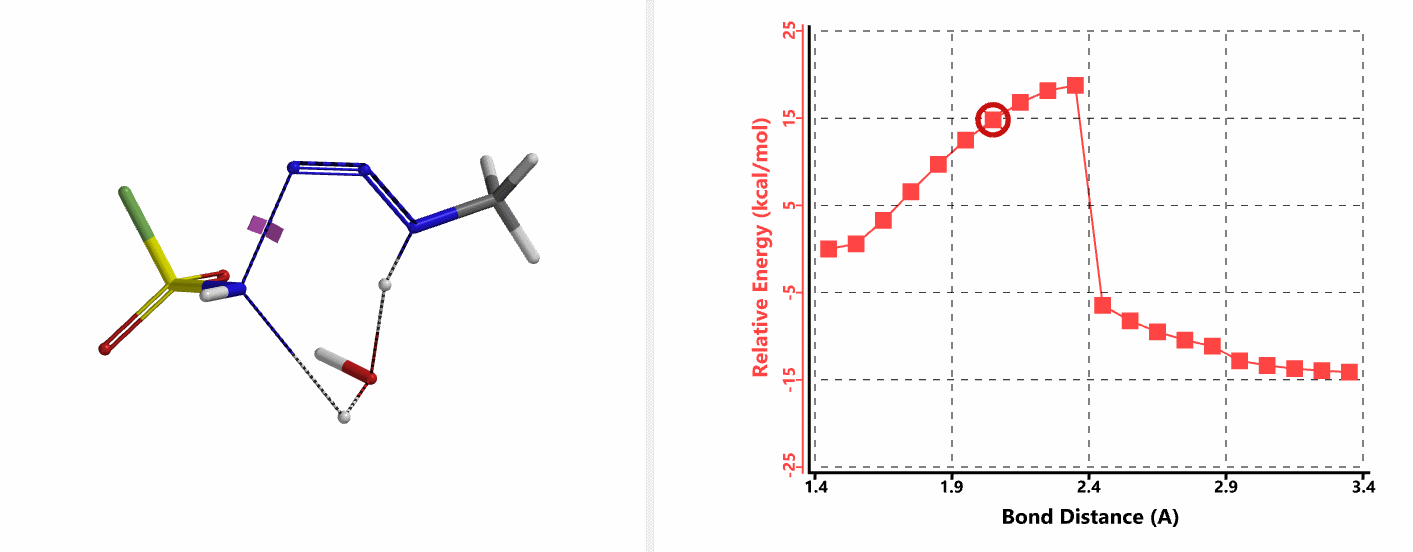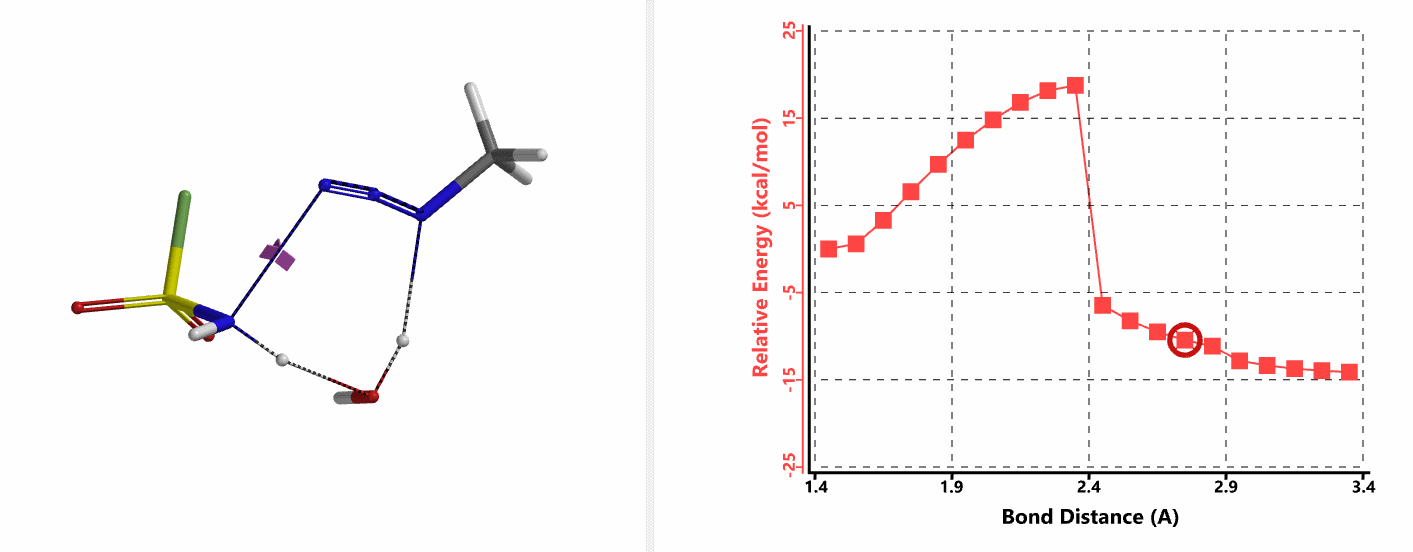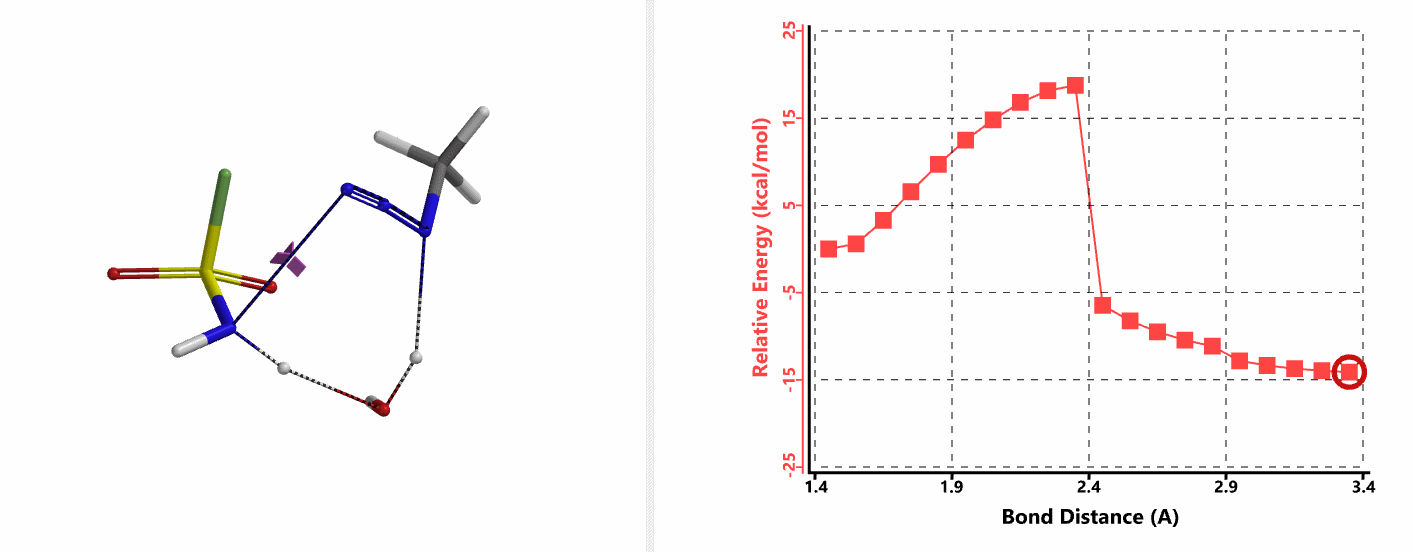
图9 磺酰氟叠氮N-N键断裂，氢原子转移并生成终产物的势能变化曲线

我们将起始物种的相对能量设为零，得到的反应中间体及过渡态的能量绘制在一张图中，即得到了这个叠氮转移反应的势能剖面图，如图10所示。我们可以看到，反应的各个分步的能垒都很低，产物具有最低的能量，并且最后一个步骤的逆向过程会有约有30 kcal/mol的能垒，这样的差值意味着整个反应进程在室温下是不可逆的^[4]。

图10 叠氮转移反应的势能剖面图

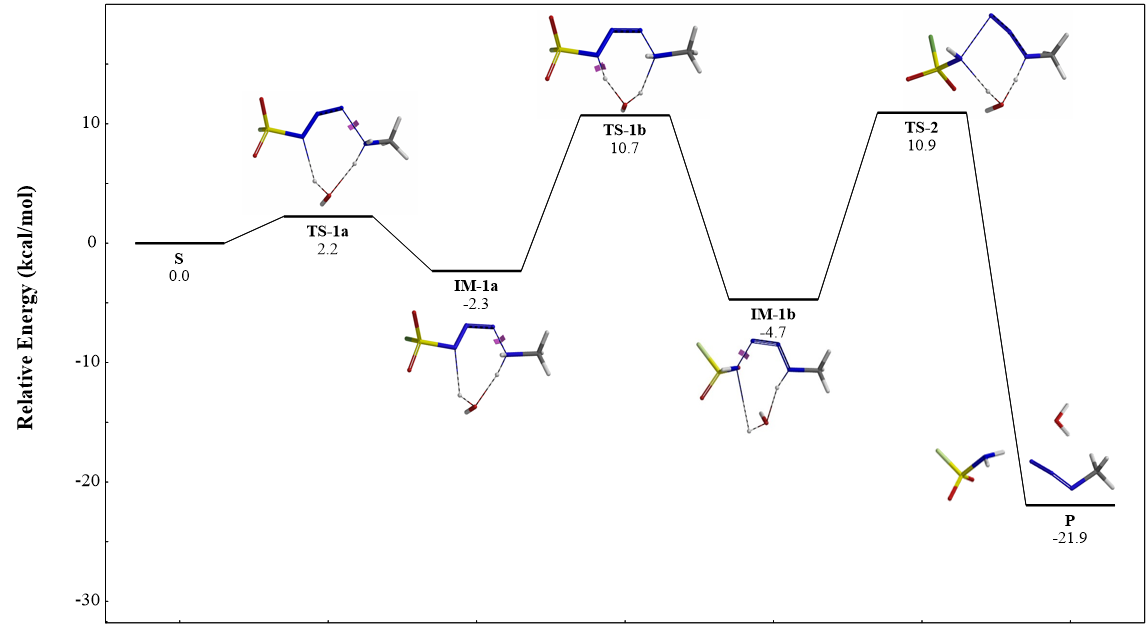
这个例子展示了一个通过QM计算来推测反应历程的完整过程。首先，我们根据经验得出可能的机理和分步反应的第一个过渡态，并通过活化能计算得到该步反应的势能变化曲线，并通过频率分析的手段，验算虚频对过渡态的合理性进行进一步的确认。接下来我们以该过渡态产物的构型出发，重复上述这一过程，直到反应的过渡态能够导向最终产物，同时也再一次指出水在反应中的重要作用。这为我们系统的研究反应机理提供了一个得力的手段，希望大家能从这个例子中得到借鉴，并应用到自己的工作中去。

小试牛刀

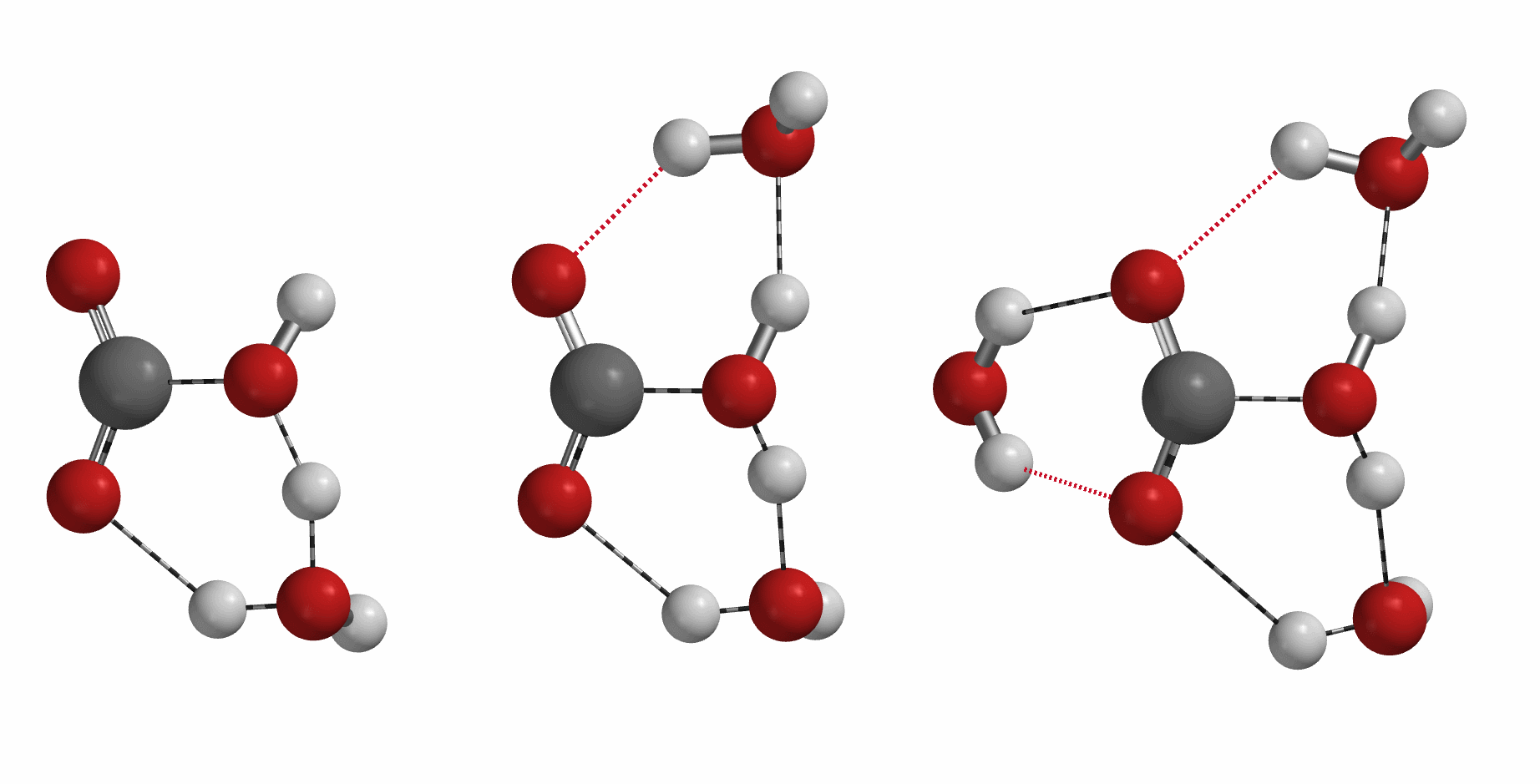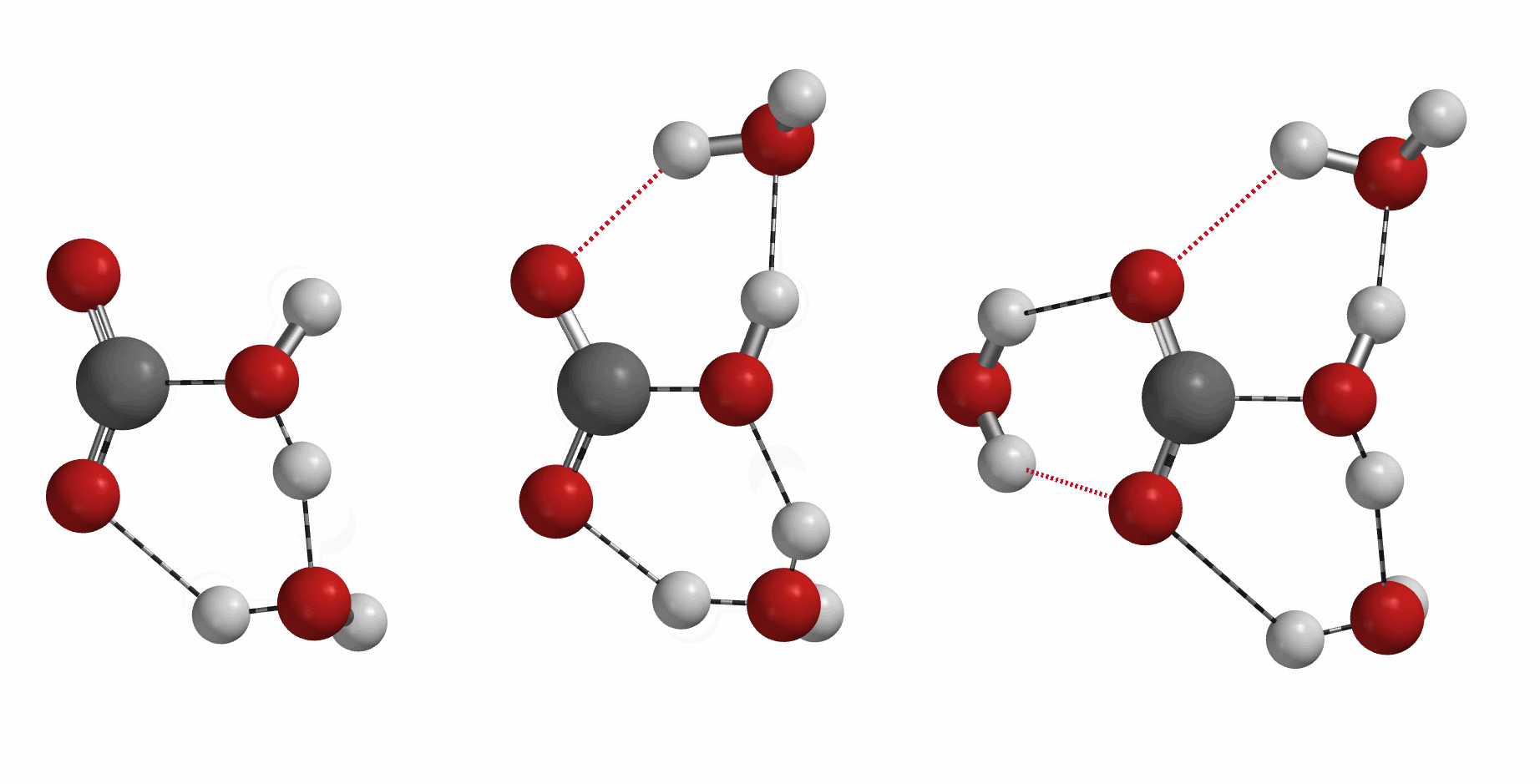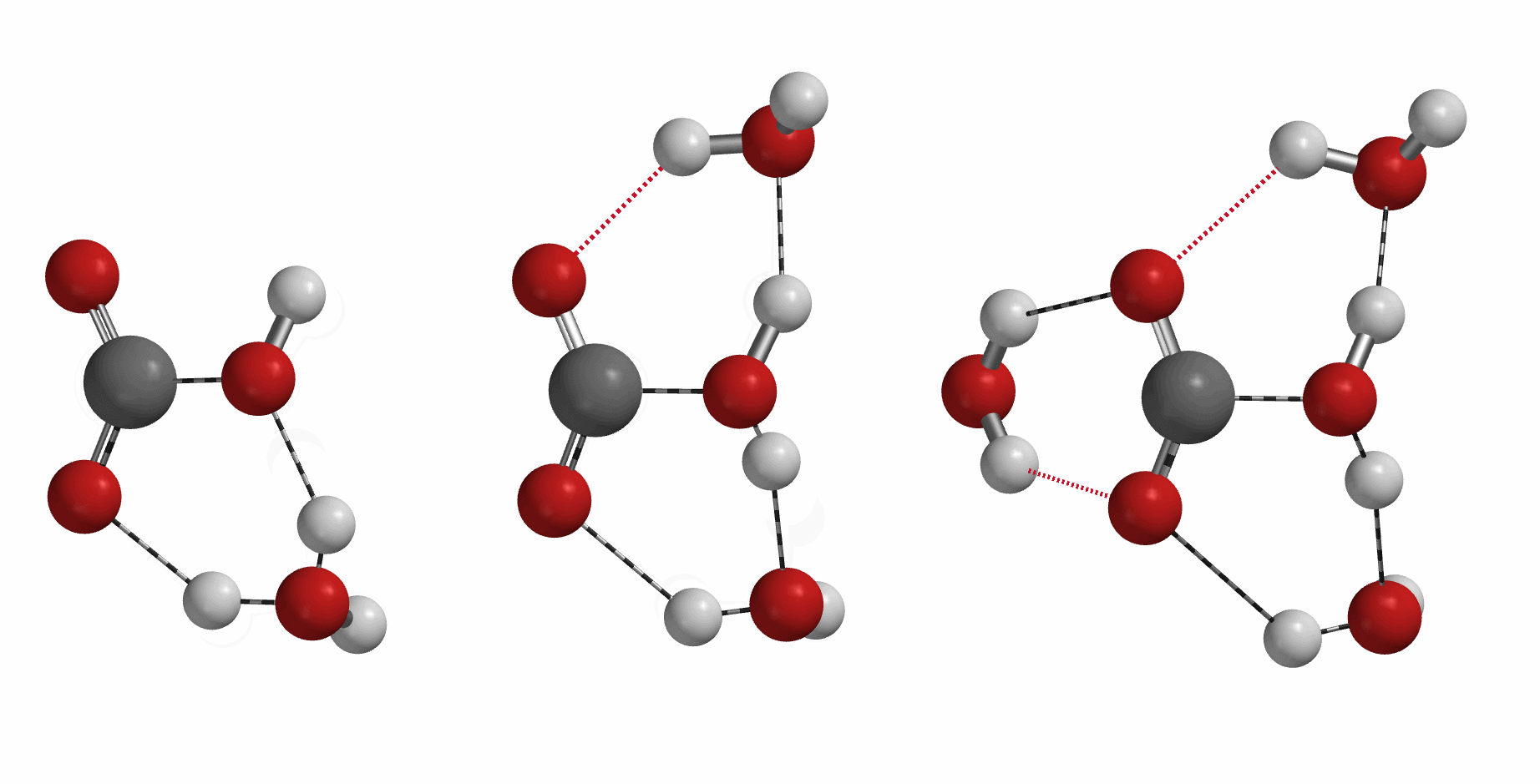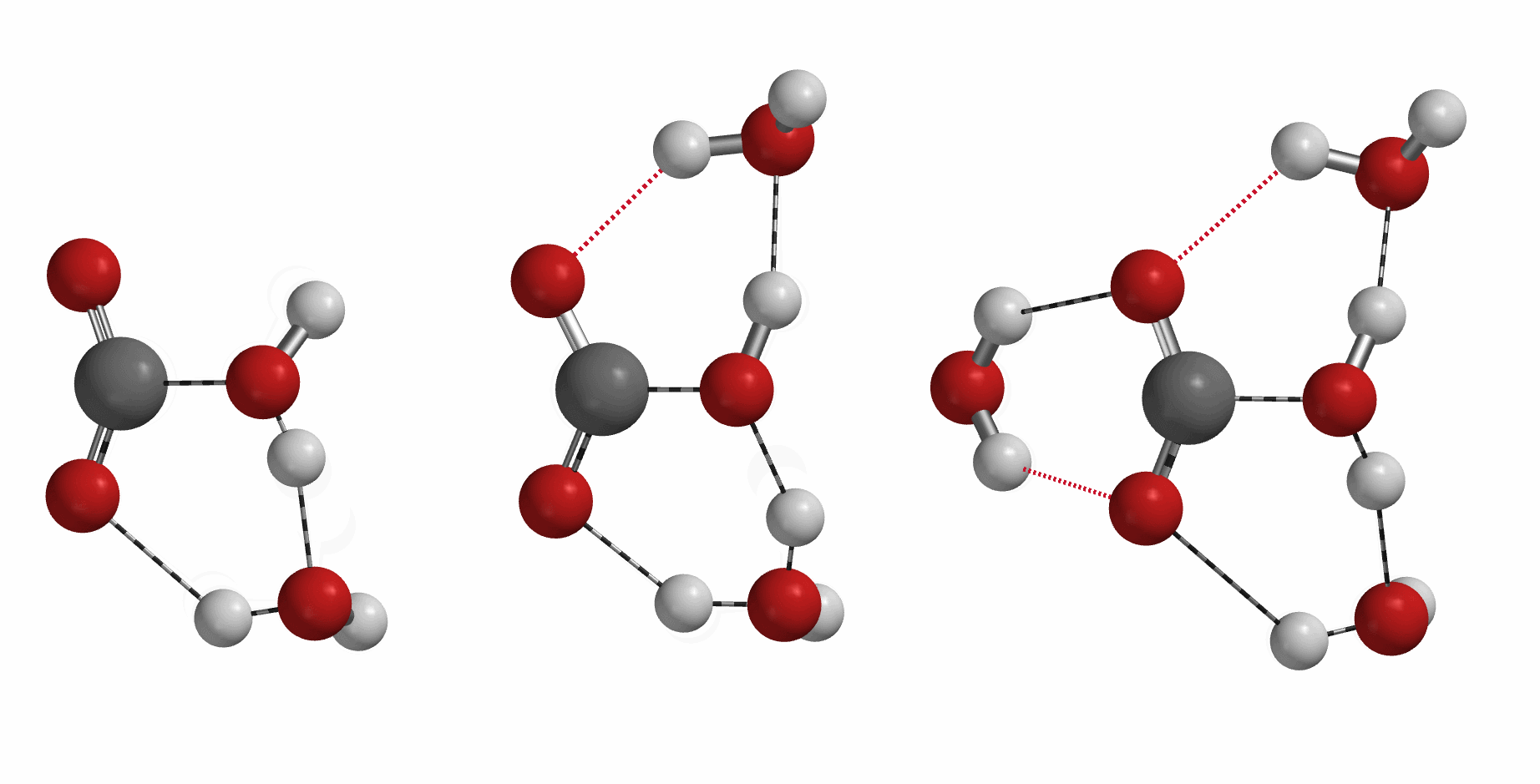
大家都知道，二氧化碳和水反应会生成碳酸，一个常见但不可或缺的反应。那么你知道在一分子碳酸形成过程中，有几个水分子参与么？^[5][6][7]

开动大脑，留言反馈，神秘大奖等着你！

iFreq 732 cm-1 iFreq 1032 cm-1 iFreq 39 cm-1

(Irrelevant vibration)

参考文献:

[1] Jiang, X.; Hao, X.; Jing, L.; Wu, G.; Kang, D.; Liu, X.; Zhan, P. Expert Opin Drug Dis 2019, 14 (8), 779–789.

[2] Meng, G.; Guo, T.; Ma, T.; Zhang, J.; Shen, Y.; Sharpless, K. B.; Dong, J. Nature 2019, 574 (7776), 86–89.

[3] Pandiakumar, A. K.; Sarma, S. P.; Samuelson, A. G. Tetrahedron Lett 2014, 55 (18), 2917–2920.

[4] Young, D. C. Computational Chemistry: A Practical Guide for Applying Techniques to Real-World Problems, 2001.

[5] Nguyen, M. T.; Raspoet, G.; Vanquickenborne, L. G.; Duijnen, P. T. V. J Phys Chem A1997, 101 (40), 7379–7388. (Molecular Orbital Model: water self-catalysis, n = 3)

[6] Lam, R. K.; England, A. H.; Sheardy, A. T.; Shih, O.; Smith, J. W.; Rizzuto, A. M.; Prendergast, D.; Saykally, R. J. Chem Phys Lett 2014, 614, 282–286. (First Principle Molecular Dynamic Model and x-Ray Absorption Spectroscopy: hydration number = 3.17)

[7] Lindskog, S. Pharmacol Therapeut 1997, 74 (1), 1–20. (Zn++ catalysis, n = 1)

本文由郑重、王秋月、王健、卫小文编撰。