硝化反应是有机合成化学中常见的反应，目前常用的硝化方法很多。Menke Nitration最早由Menke于1925年报道^[1]，是指用硝酸铜和乙酸酐条件对芳香族化合物的硝化，目前文献报道的反应机理如图1所示^[2]。

图1. 可能的Menke Nitration反应机理

1960年F. G. Bordwell等^[3]发现在硝酸—乙酸酐的硝化体系中烯烃可以和AcONO₂发生硝化反应，并提出质子化的硝酸乙酰酯 (AcOHNO₂)⁺可能是硝化的活性物种。受此启发，我们推测在Menke Nitration中真正参与硝化的是AcONO₂而不是NO₂⁺。今天，我们将利用QM来探索这一猜想是否正确。

反应机理探讨

根据这种假设，我们提出了如下两种可能的反应机理 (图2)。首先，硝酸铜与乙酸酐反应生成中间体AcONO₂。Path 1是中间体AcONO₂与苯环进行亲电取代反应，之后H⁺离去形成产物并失去一分子乙酸。Path 2则是直接通过分子内氢键形成六元环过渡态一步得到产物。

图2. Menke Nitration两种可能的反应机理

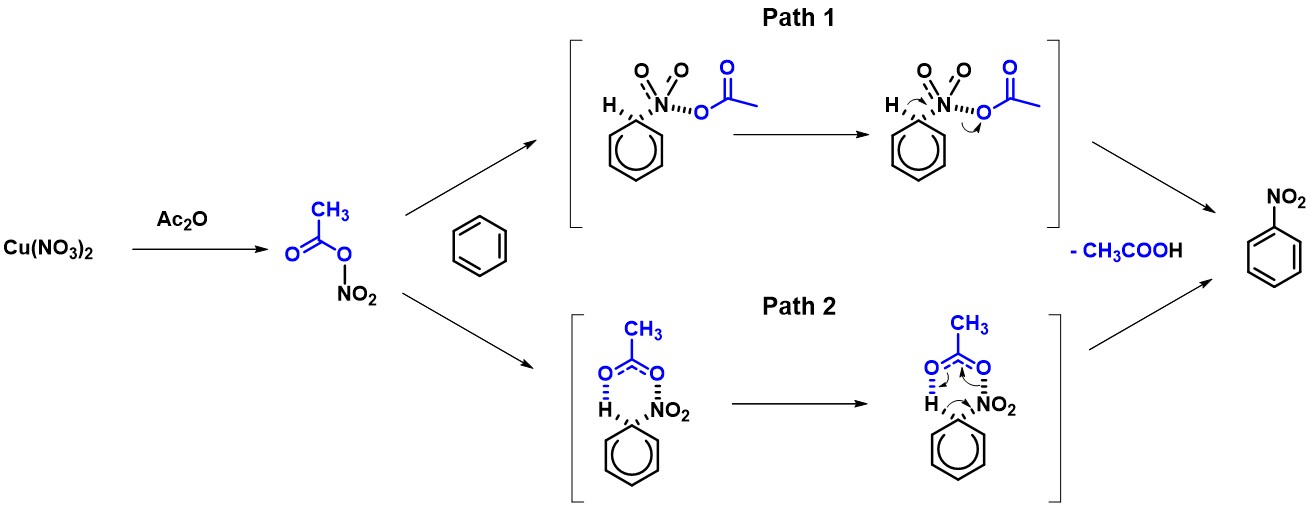
接下来，我们通过QM计算两种不同机理相应的过渡态和活化能来论证哪个反应机理更合理。首先我们建立QM计算模型，将C-N的距离变化设定为从彼此无相互作用的3.0 Å到共价键的成键距离1.5 Å，步长为0.1 Å。通过模拟，我们计算得到经由Path 2的活化能约为50 kcal/mol，比通过Path 1途径的活化能低了约10 kcal/mol (图3)。这表明通过分子内氢键形成六元环过渡态一步得到产物需要的能量更低，反应更容易通过Path 2发生。

图3. 两种可能反应机理的能量变化曲线

我们分别选取两个过程中能量最高点的结构TS1和TS2，选择Transition State Geometry计算更精确的过渡态结构和相对能量。计算结果表明TS2的能量要比TS1低7.09 kcal/mol，TS2分布比例达到了100% (图4)。这可能是由于氢键的存在进一步稳定了TS2结构，降低了其能量。

图4. TS1和TS2的相对能量和所占比例

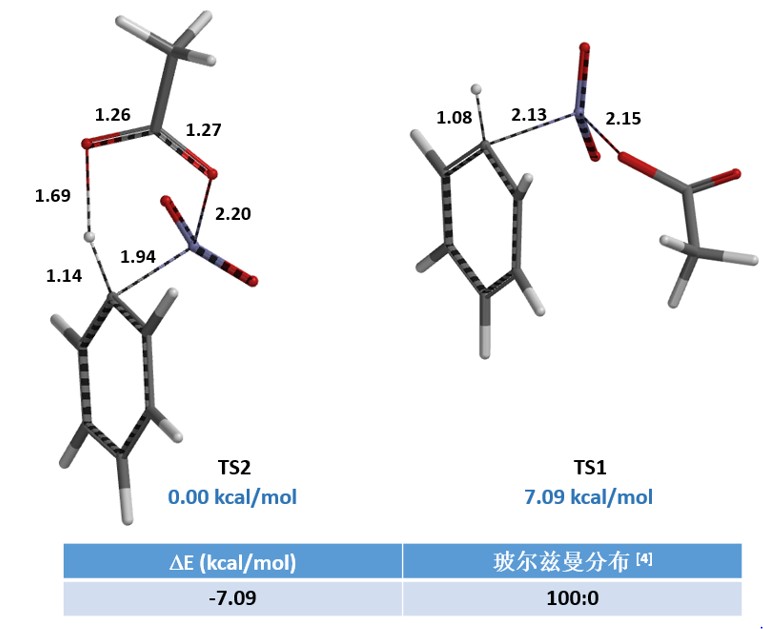
接着，我们选取结构TS2进一步计算红外振动，结果表明该结构有且只有一个虚频 i412 cm^-1 (图5)^[5]，这进一步支持了TS2为Menke Nitration的反应过渡态。由此我们认为Menke Nitration是AcONO₂和芳环反应经过一个六元环过渡态的硝化机理。

图5. 反应能量变化曲线，TS2过渡态及IR计算摘要

反应机理的运用

接下来，我们来看一个上述反应机理的运用实例。化合物1发生硝化反应得到的是6位和8位硝化的混合物，两者的比例为3:1。我们将利用这个例子来回顾QM的应用方法，并通过这些方法来分析Menke Nitration的区域选择性。

图6. Menke Nitration实例

芳环的硝化是亲电取代反应，首先通过QM计算它的HOMO和¹³C NMR (见第2章)。为方便计算将化合物的R基团简化为甲基，结果如图7所示。C-6的HOMO lobe明显大于C-8位。但是能量相近的HOMO-1中，C-8的lobe分布又明显大于C-6。同时，¹³C NMR计算显示C-6 (108.2 ppm)与C-8 (104.8 ppm) 位移值差 < 6 ppm。故我们预测会得到2A和2B的混合物，2A为主产物。

图7. 化合物1的HOMO, HOMO-1 & ¹³C NMR示意图

接下来借助前面提出的Menke Nitration的反应机理，计算活化能，寻找反应过渡态，通过两者活化能的差值就可以计算两种产物的比例。第一步，我们利用QM建立模型，并计算C-6位和C-8位的活化能分别为38.7 kcal/mol 和42.6 kcal/mol，说明硝化更容易发生在C-6位上。

图8. C-6 & C-8硝化的过渡态结构

然后我们分别选取两个过程中能量最高点，选择Transition State Geometry计算得到过渡态TS6和TS8（图8）。在气相环境下两者相对能量差值约为4.31 kcal/mol。

由于Menke Nitration是发生在醋酸体系中，所以气相计算结果与实验结果不一致，需要选择非气相环境进行计算 (表1)。计算表明选择Polar solvent结果更为准确，与我们的实验结果3:1非常接近。这也进一步验证了我们猜想的Menke Nitration过渡态是AcONO₂和芳环反应经过一个六元环过渡态的硝化机理。

表 1. 不同环境下计算得到的产物比例

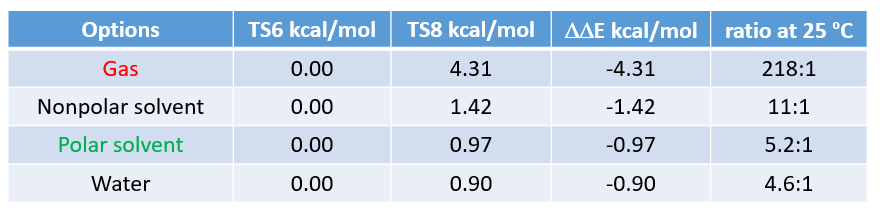
这一案例展示了我们如何通过QM的计算来分析论证反应机理。首先，我们根据经验给出可能的机理，通过能量变化曲线找到过渡态结构，计算虚频进行确认。同时将计算结果应用到实际案例中，与实验结果进一步比较来验证我们的计算是否正确。这就为我们合理解释反应现象、有效解决合成工作中的实际问题提供了一项有力的新手段，也希望这些分享能为大家带来更多启发。

小试牛刀

通过QM计算，Menke硝化反应中的AcONO₂的LUMO能量为 -0.29 eV (图9)。而anhydrous HNO₃与发烟硫酸中的SO₃反应生成的HSO₃ONO₂的LUMO能量为 -1.00 eV，具有更强的亲电能力，可以在70-90度相对较低温度下用于二硝基甲苯的连续、闭环硝化制备TNT^[6]。请参考本章内容，HSO₃ONO₂对苯进行硝化的能量变化曲线 (图10)，和过渡态结构计算虚频 i194 cm^-1, 评估HSO₃ONO₂硝化反应是否也是通过一个六元环过渡态。

图9. AcONO₂和HSO₃ONO₂的LUMO和LUMO map

图10. HSO₃ONO₂硝化苯的能量变化曲线

参考文献：

[1] (a) Menke, J. B. Recl. Trav. Chim. Pays-Bas, 1925, 44, 141. (b) Menke, J. B. Recl. Trav. Chim. Pays-Bas, 1925, 44, 269. (c) Menke, J. B. Recl. Trav. Chim. Pays-Bas, 1925, 44, 270.

[2] Wang, Z. Comprehensive Organic Name Reactions and Reagents, volume 2. John Wiley & Sons, Inc., Hoboken, New Jersey, US, 2009, 1893.

[3] Bordwell, F. G., Garbisch, E. W. Jr. J. Am. Chem. Soc., 1960, 82, 3588.

[4] 玻尔兹曼分布函数描述了在热平衡下，分子按能量高低的概率分布。

[5] Spartan '18 Tutorial and User's Guide (2019). Irvine, CA, USA: Wavefunction, Inc. pages 152, 495 & 613. 在量子计算中，过渡态附近的分子振动可以近似为谐振子模型来描述。如下方程所示，振动频率与力学常数 k 除以原子折合质量的开方成正比。力学常数 k 反应的就是势能面沿着特定坐标的曲率 (由能量相对于几何坐标的二阶导数定义)。在第八章中介绍了过渡态理论，过渡态处于势能面上的马鞍点位置。其数学含义是只在反应路径方向上具有极大值，而其他方向都是极小值。在反应路径上过渡态的曲率为负值 (极大值的二阶导数为负)，质量为正值，所以开方后计算频率得到一个虚数，即文中提到的虚频。所以通过有且仅有一个虚频就来确定结构处于鞍点位置，即是我们寻找的过渡态。

[6] Hill, M. E., Tolber, W. E., McDonald, G. J. US Patent 3,799,993, March 26, 1974.

本文由沈小莉、赖光华、潘东、陈永胜、卫小文编撰。