网站维护
系统内容更新/升级中

立体选择性在有机合成反应中至关重要。提到影响产物立体构型的因素,日常考虑比较多的有电性因素,位阻因素,超共轭因素等等。本章节我们会分享一种在立体构型生成过程中起着重要作用,在早期被化学家们称为“神秘因素”——Factor X。
想知道Factor X的真面目?快跟上我们的节奏,一起揭晓答案!
我们从一个实例出发:
大家都知道降冰片烯的环氧化反应会高选择性地得到exo产物,如图1所示。
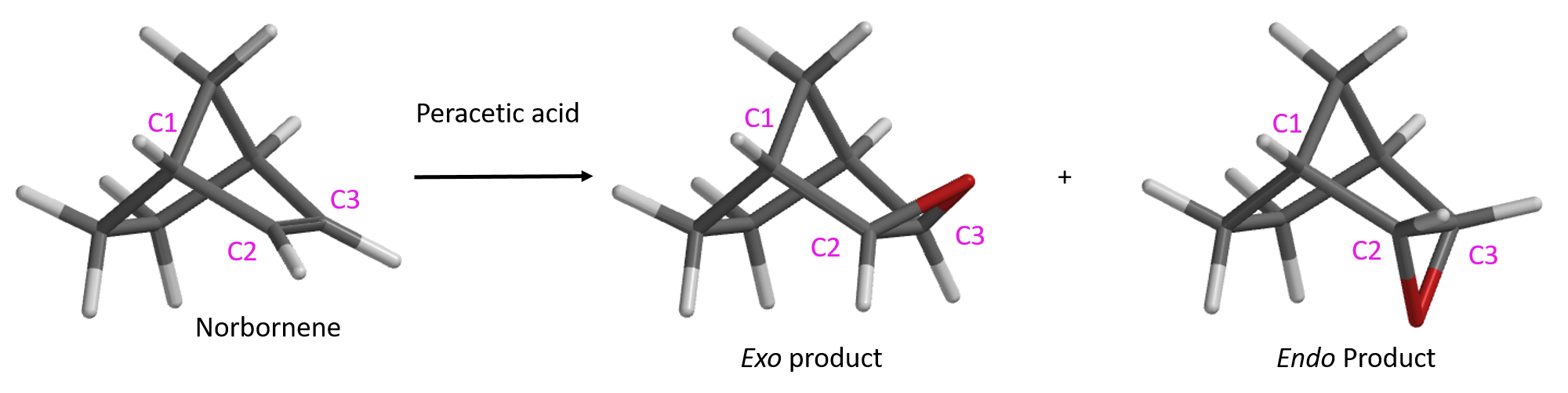
我们根据Prilezhaev Reaction的反应机理进行QM计算模型构建:以降冰片烯为反应底物,过氧乙酸分别从上/下两面进攻,模拟过氧乙酸-O与双键两端C2、C3原子O-C键的形成。以图2中从下面进攻生成endo产物为例,定义O-C之间的距离,从彼此远离的3.2 Å逐渐接近至进入共价键作用范围的1.9 Å。基于O-C2与O-C3键在形成过程有同步对称效应,后文为了便于观察,我们只对O-C2一面进行讨论。
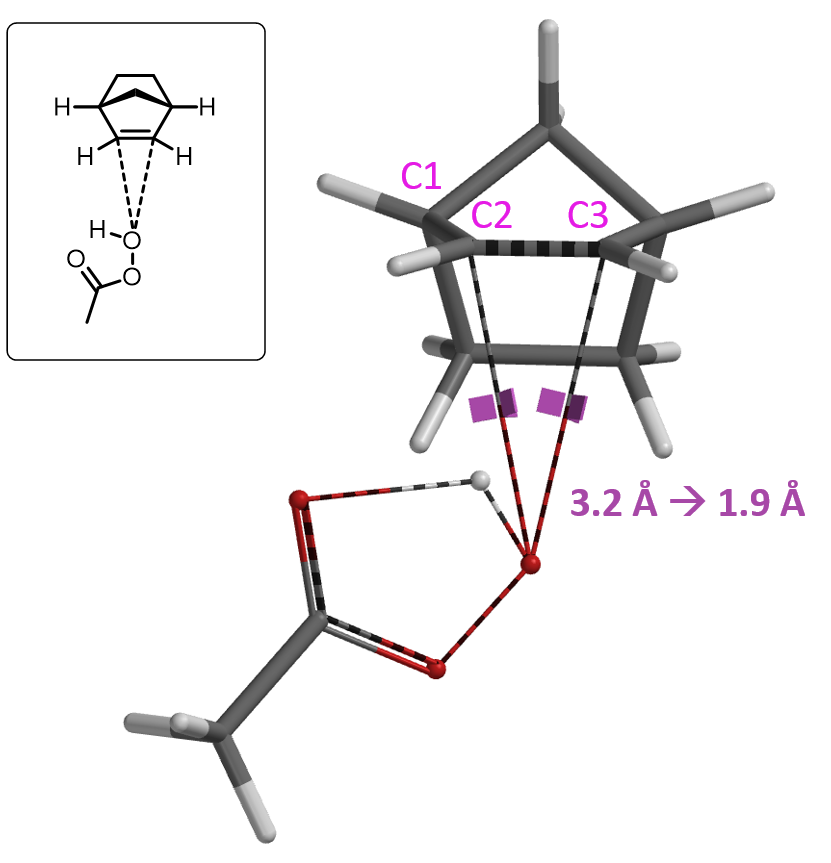
通过QM计算可以得知 (图3所示) ,过氧乙酸从上面进攻生成exo产物的活化能ΔE = 22.33 kcal/mol,而通过从下面进攻生成endo产物的活化能ΔE = 26.95 kcal/mol。二者差值为ΔΔE = 4.62 kcal/mol,这表明如果反应在25 ℃进行,基本只能观察到exo产物。
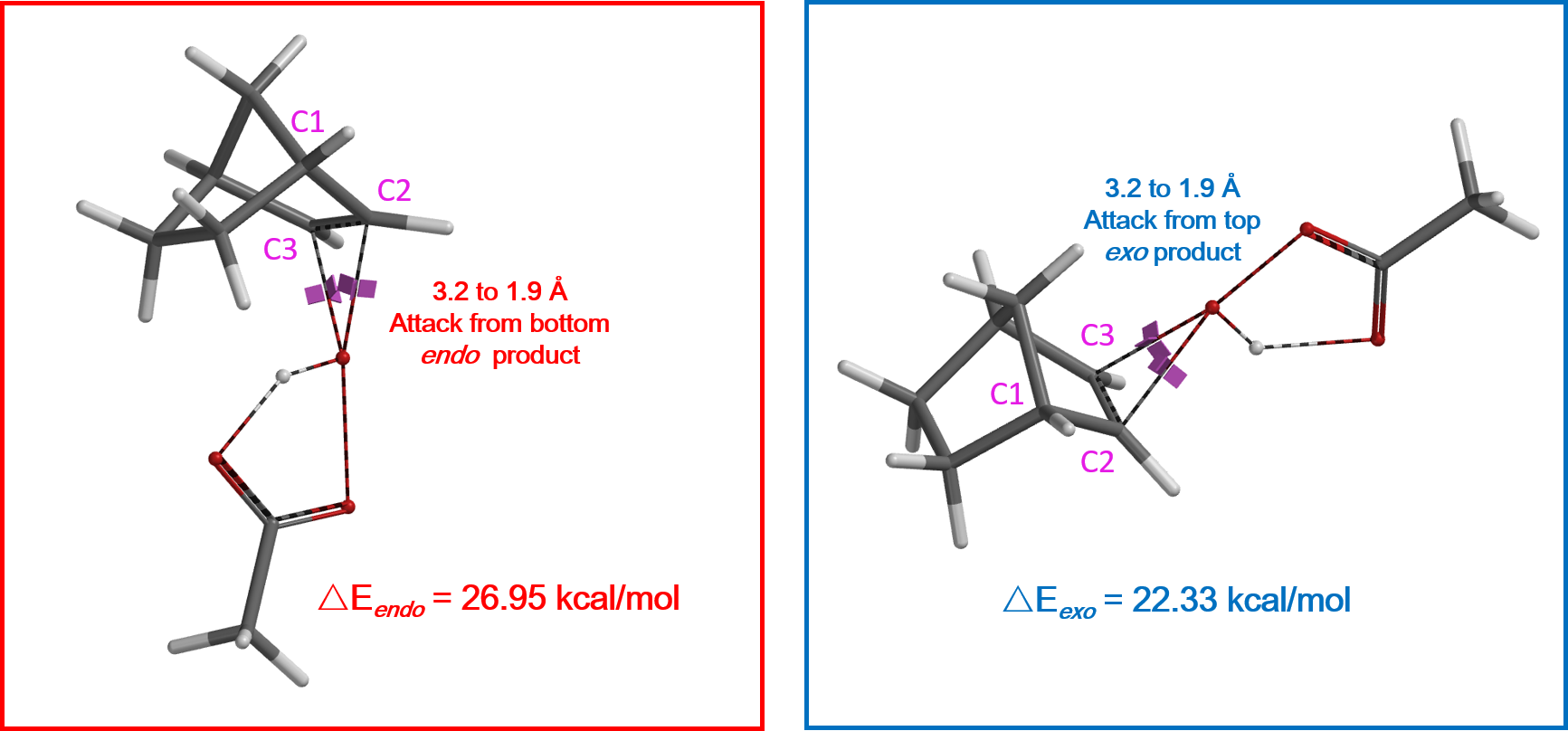

那么问题来了!是什么原因导致这4.62 kcal/mol的能量差呢?
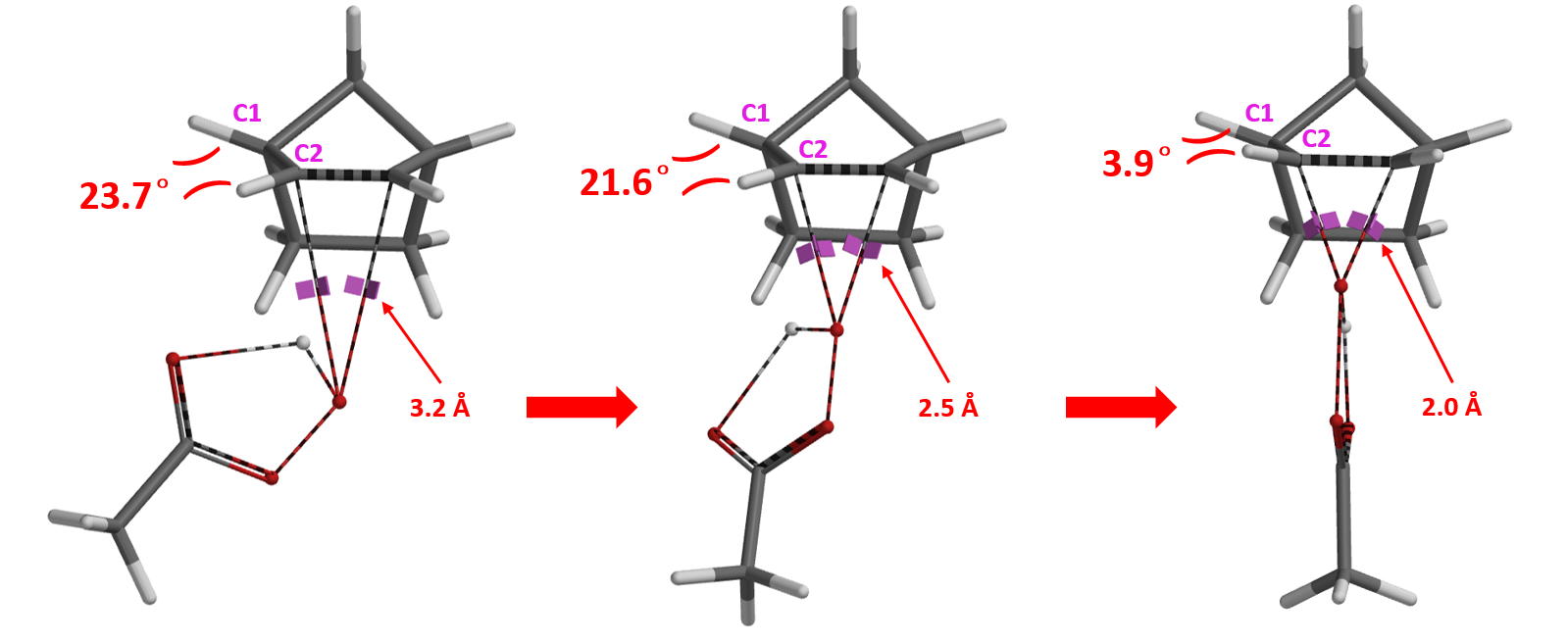
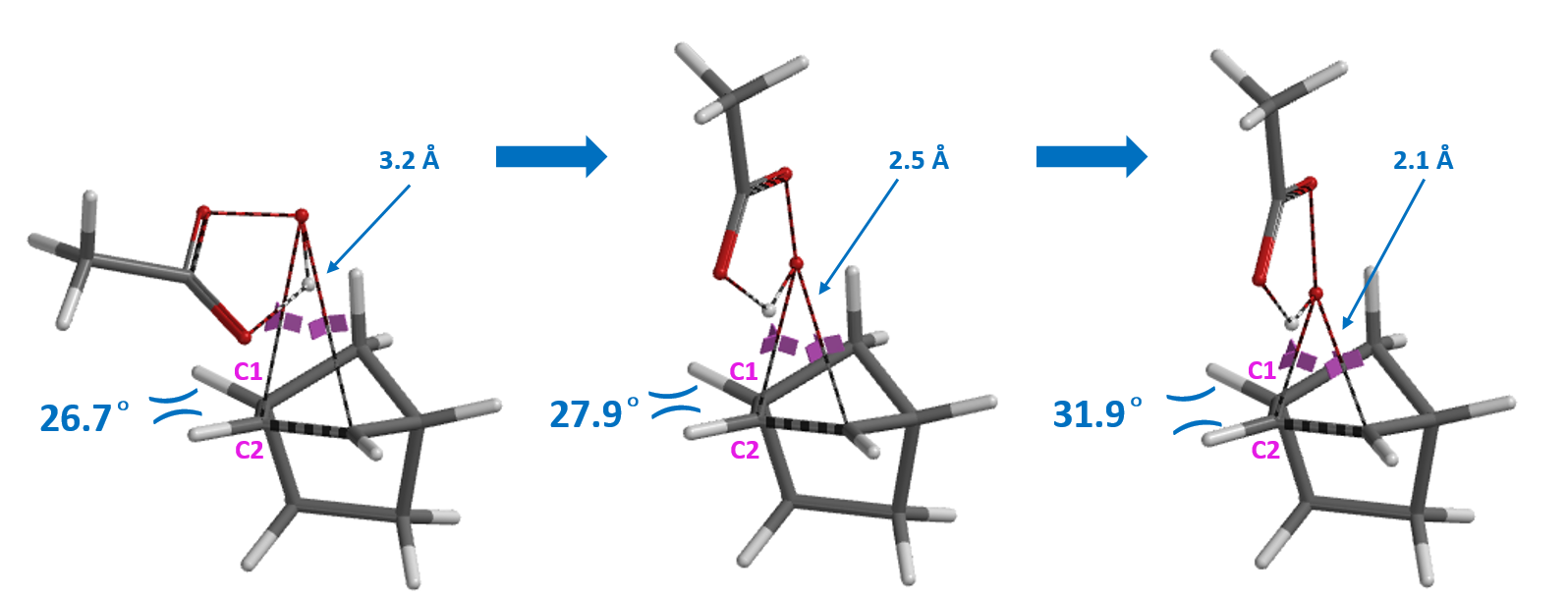
我们分别选取O-C键长为3.2 Å, 2.5 Å, 2.0 Å/2.1 Å时的结构,观察反应初始状态、反应进行中、过渡态结构。如图4所示,当过氧乙酸从下面进攻时,随着反应的进行,C1-H与C2-H有互相靠近、形成空间位阻的趋势;从上面进攻,C1-H与C2-H会有一个彼此远离、舒缓空间位阻的趋势。这个现象所体现的,就是我们要分享的本章的主角——扭转张力(torsional strain),它就是早期被化学家们称之为Factor X,影响产物立体构型的一个重要因素!
从下面进攻生成 endo 构型产物:
从上面进攻生成 exo 构型产物:
扭转张力(torsional strain)是构象分析中的一种术语。我们在课本中学过乙烷在常温下存在交叉式与重叠式两种极限构象,前者较后者内能低而稳定,因而后者极易转变为前者,这种分子内在的转变力称为扭转张力。
同时我们知道,在立体化学中,分子每三个非共线的原子都决定了一个平面,当两个这样的平面相交时,他们之间的角度称为二面角,也叫扭转角。如果二面角角度相对较大,则扭转张力相应较小,二面角角度趋小,则扭转张力会趋大。
对于具有扭船式稳定构象的降冰片烯来说,我们这里主要考虑烯键的C2-H键与邻位C1-H键在反应过程中的作用力。从图4中可以看到,从下面进攻(endo attack),C1-H与C2-H键的二面角(23.7°)逐渐变小,形成几乎重叠式(3.6°)的过渡态;相比之下,从上面进攻(exo attack),C1-H与C2-H键的二面角反而逐渐增大,从26.7°扩大到31.9°,形成交叉式的过渡态结构。烯键另一端也同时有类似的扭转张力影响及二面角变化。正是因为重叠式与交叉式相比具有更大的扭转张力,导致endo产物所需活化能比exo产物高出4.62 kcal/mol。
利用QM计算模拟反应进程,观察扭转角度,可以分析高选择性立体异构体生成的原因,也可用于路线设计中合成立体异构优势产物的策略应用。
小伙伴们想一想日常实验是否碰到过其它以扭转张力为主要影响因素的反应?大家可以通过QM计算来直观感受其中的乐趣!
我们在正文举例了一个烯键的环氧化故事,那么扭转张力在环氧化合物的开环反应中是否也会扮演重要角色呢?这里,我们留下一个小题,供您思考:
当亲核试剂进攻C2位,我们需要考虑C2-H与邻位C1-H的扭转张力;
当亲核试剂进攻C3位,我们需要考虑C3-H与邻位C4-H的扭转张力。

温馨小提示:
下一章我们将继续分享用量子力学计算的方法来分析立体异构的案例,相信能给您带来更多的收获!敬请期待!
本文由王秋月、石谷沁、卫小文编撰。
参考文献:
[1] Warren J. Hehre (2003). A Guide to Molecular Mechanics and Quantum Chemical Calculations. Irvine, CA, USA: Wavefunction, Inc.
[2] H. Wang & K. N. Houk, Chem. Sci. 2014, 5, 462.